I'm trying to read a lot of ML papers at the moment but I have to admit I find a lot of the language alien. Sometimes I have this fantasy that it's all familiar stuff but buried under unfamiliar notation and I just need to unlock it with the right key.

Anyway, here's a nice example where that assumption paid off:

There's an important result about "denoising autoencoders" here: https://www.iro.umontreal.ca/~vincentp/Publications/DenoisingScoreMatching_NeuralComp2011.pdf

There's this quasimagical step where you need a derivative of a smooth field but you have no access to the field, just values at a scattered set of points, and yet they get the derivative by introducing a new random variable.

Then it clicked.

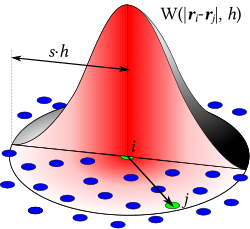
This is smoothed particle hydrodynamics in disguise. In SPH you simulate fluids with lots of particles and you get fields by splatting a little Gaussian kernel over every particle and summing them all. Now you can take the derivative.

The notation is very different, and so is the language of conditional and marginal probabilities. But it's much the same method. A Gaussian kernel around every data point.

Compare https://en.wikipedia.org/wiki/Smoothed-particle_hydrodynamics