Greg Egan @gregeganSF@mathstodon.xyz
Public

Gravity is the curvature of spacetime. So, how curved is the spacetime we are in right now?

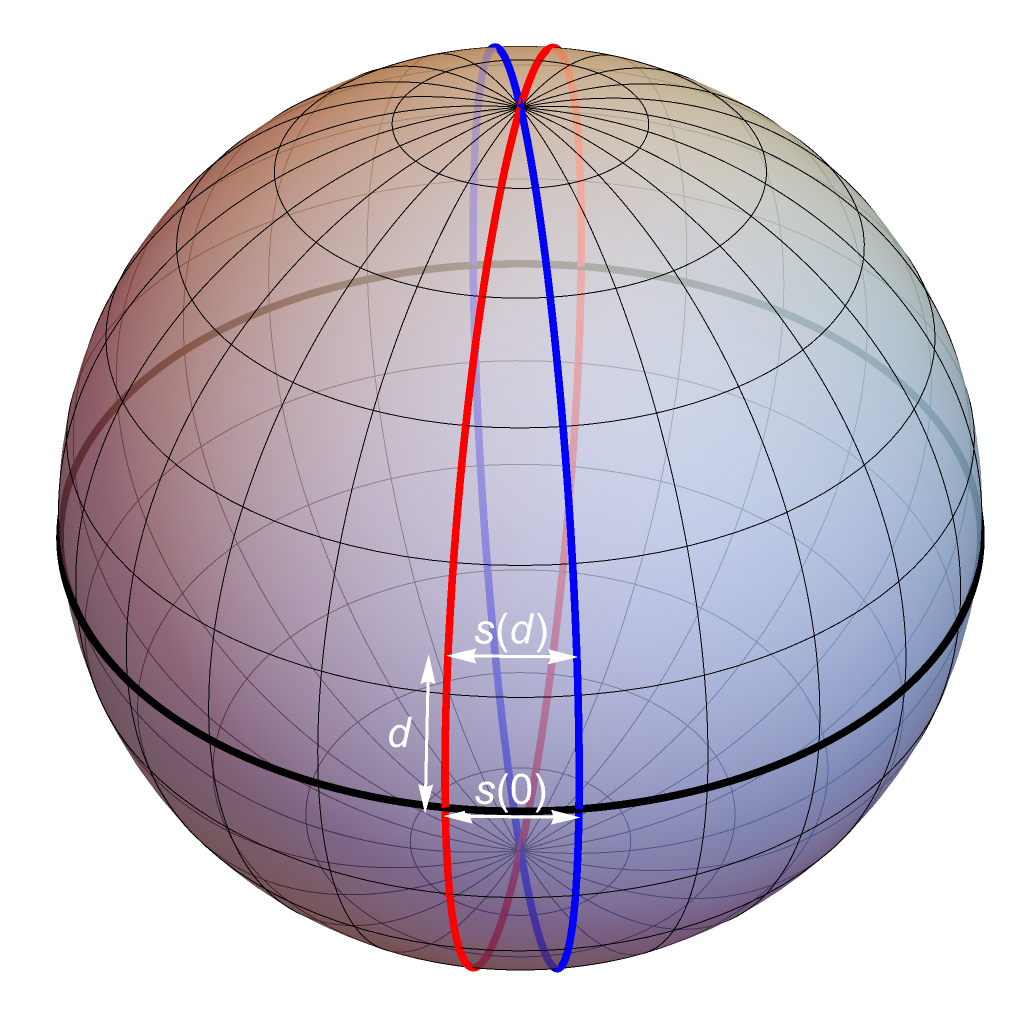
Let’s start by looking at the effect of curvature in a very simple situation. Two meridians on a sphere, like the red and blue ones in the diagram, will come together and move apart as you follow them along their length. If their separation at the equator is s(0), after a distance d it will be:

s(d) ≈ s(0) cos(d/R)

where R is the radius of the sphere. The separation will repeat with a period of P = 2πR, so we can say that the radius of curvature of the space these geodesics are in is:

R = P / (2π)

A sphere, with one meridian coloured red and a nearby meridian coloured blue. The separation between them at the equator is labelled s(0), while the separation a distance d up from the equator is labelled s(d).
0
0
0

If you have a fediverse account, you can quote this note from your own instance. Search https://mathstodon.xyz/users/gregeganSF/statuses/115876082707595495 on your instance and quote it. (Note that quoting is not supported in Mastodon.)