John Carlos Baez @johncarlosbaez@mathstodon.xyz
Public

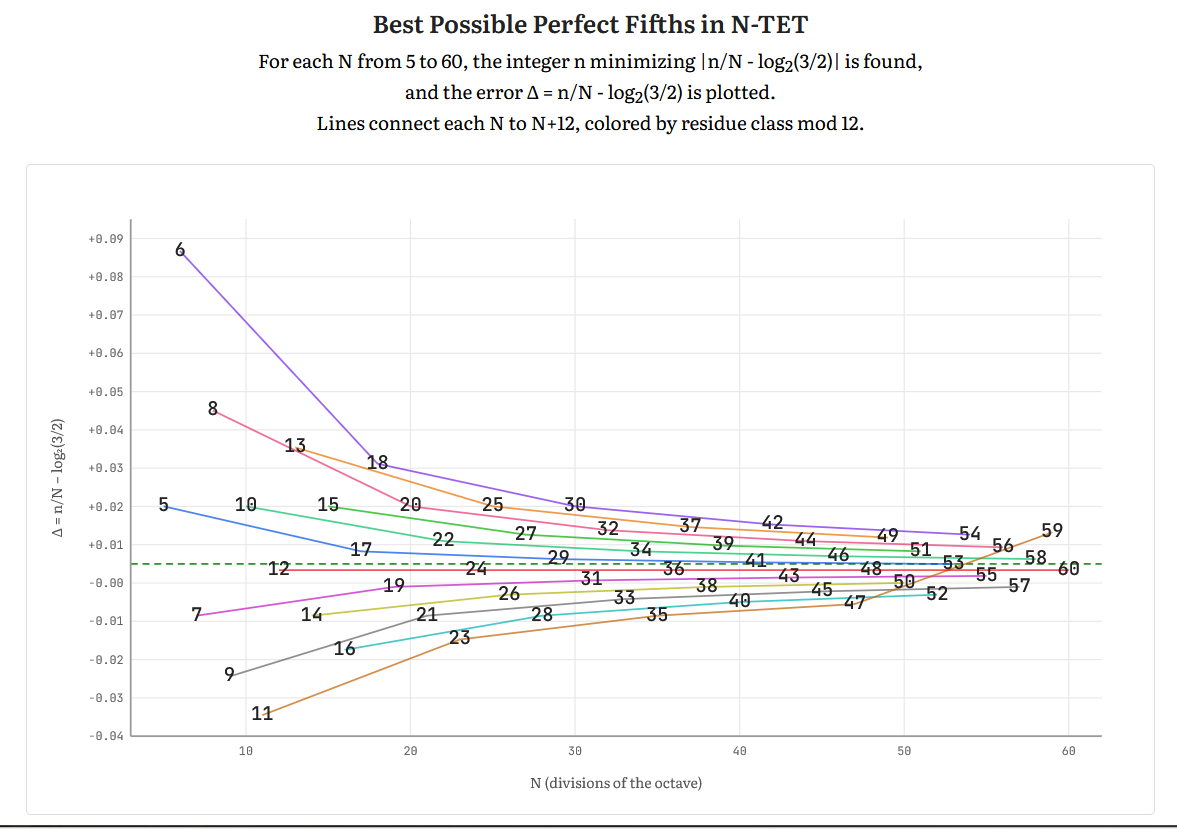
Take a scale where the octave is divided into N equal parts. See how close you can get to a 'perfect fifth': a frequency ratio of 3/2. Plot the error as a function of N. You get a complicated pattern...

... but if you draw 12 colored lines through the different values of N mod 12, you get this!

So don't let anyone tell you the role of the number 12 in musical scales is purely a cultural artifact: it's built into the math!

Please don't be put off by the jargon: 'N-TET' means 'N-tone equal temperament', which means a scale where the octave is divided into 12 equal parts. Most pianos use 12-TET.

You can see an interactive version of this here:

math.ucr.edu/home/baez/tuning_

Best Possible Perfect Fifths in N-TET For each N from 5 to 60, the integer n minimizing |n/N - log_2(3/2)| is found, and the error Δ = n/N - log_2(3/2) is plotted. Lines connect each N to N+12, colored by residue class mod 12. We get 12 different curves, mostly rather smooth, except that one pops up as it goes from N = 47 to N = 59. All this can be explained....
0
0
0

If you have a fediverse account, you can quote this note from your own instance. Search https://mathstodon.xyz/users/johncarlosbaez/statuses/116110277149045694 on your instance and quote it. (Note that quoting is not supported in Mastodon.)