Hackers' Pub is a place for software engineers to share their knowledge and experience with each other. It's also an ActivityPub-enabled social network, so you can follow your favorite hackers in the fediverse and get their latest posts in your feed.
Local SEO vs. National SEO vs. Global SEO: A Strategy Guide https://www.semrush.com/blog/local-seo-vs-national-seo/
i'm sorry i don't have the capacity to react to every horror that is happening in real time
i'm sorry i don't have the capacity to react to every horror that is happening in real time
ハーフドロ
Combing through the ActivityPub, ActivityStreams, and JSON-LD specifications to clean up my interpretation of the ActivityPub primitives. Finding I might need a new Lexicon primitive to correctly handle/constrain the `@context` terms dictionary in JSON-LD. Can hack-it for now though. #atproto #atdev
Go make ugly websites.
>Soon it will become something else entirely. Because it’s my website and I’m perpetually becoming somebody else.
> You’ll change too. Your passions and values will pollinate; your ugly thing – whatever it is – will come alive again and again.
https://goodinternetmagazine.com/my-website-is-ugly-because-i-made-it/
일어났어요
DHS Releases Statement on Violent Rioters Assaulting ICE Officers in Los Angeles, CA and Calls on Democrat Politicians to Tone Down Dangerous Rhetoric About ICE (Department of Homeland Security)
https://www.dhs.gov/news/2025/06/07/dhs-releases-statement-violent-rioters-assaulting-ice-officers-los-angeles-ca-and
http://www.memeorandum.com/250607/p61#a250607p61
悲しい
「『たこ』入っていません」 物価高騰でたこ焼きがソーセージ焼きに | 毎日新聞
https://mainichi.jp/articles/20250607/k00/00m/040/231000c
今日はこれですよ
朝から4回洗濯物回した。
夢の国の代償はでかい。
あと2 回残ってるけど、干す場所ない。
そして夜にはまた日常分の2回洗濯する。
日常に復帰するのにタスクが多すぎる。
Holloのめでぃあの処理に拡張子？見てるコードあったからそのへんかねぇ
おなじだ〜
悲しい
「『たこ』入っていません」 物価高騰でたこ焼きがソーセージ焼きに | 毎日新聞
https://mainichi.jp/articles/20250607/k00/00m/040/231000c
‘저 완충까지 남은 시간 보여주기’가 드디어 아이폰에서도 다음 iOS 버전에서 “애플 인텔리전스를 기반으로” 될 거라는 *소문*이 있는데 … (안드로이드 사용자들 여러분 시간여행을 하신 게 아닙니다. 지금 2025년 맞습니다.)
2時間かけて車で行き、2時間かけて車で帰る、夢の国🏰
うおーじかんが！！おきます おきる 
Last four watched:
(Anatomy of a Fall is fucking fantastic.)
ついでにこっちも
#Fediverseサーバープロフ帳 でプロフィールカードを作成しました！ #okprint https://purofu.y-zu.org/view/server?id=173 #サーバープロフ帳 #サーバープロフィール帳 #サーバー紹介
GitLab 저장소 백업 시간을 48시간에서 41분으로 단축한 방법
------------------------------
- GitLab 은 대용량 저장소 백업 시 오래 걸리는 문제를 발견하고 개선 작업을 수행함
- 핵심 원인은 15년 된 Git 함수의 *O(N²) 복잡도* 였으며, 알고리듬 최적화를 통해 성능을 대폭 향상시킴
- 최적화 결과, 가장 큰 저장소의 *백업 시간이 48시간에서 41분* 으로 줄어듦
- 개선된 방식은 리소스 효율성과 신뢰성을…
------------------------------
https://news.hada.io/topic?id=21319&utm_source=googlechat&utm_medium=bot&utm_campaign=1834
n8n 을 좀 파볼까... 로직앱이나 파워오토메이트랑 비슷하면서도 다른 듯
개인적으로 스위치2는… 잃어버린 낭만을 좇는 일종의 노력이라고 생각함
I really liked the Talking Heads video with Saoirse Ronan for "Psycho Killer".
Motivation: Many games, especially RPGs, have a notion of "luck" which acts as a resource that players can draw from to modify die rolls. How can we make this "realistic"?
I'm fascinated by "plausible implausibility".
Stating things very informally:
Various theorems like Sanov's theorem tell you things like:
The probability that a bunch of draws from a distribution have an "extreme" empirical distribution different from the true distribution is given by the KL-divergence.
Similarly, if you know some truly preposterous sequence of draws lies in some extreme set it's most likely that the empirical distribution is at the point in the set closest to the original distribution - measured in the KL sense.
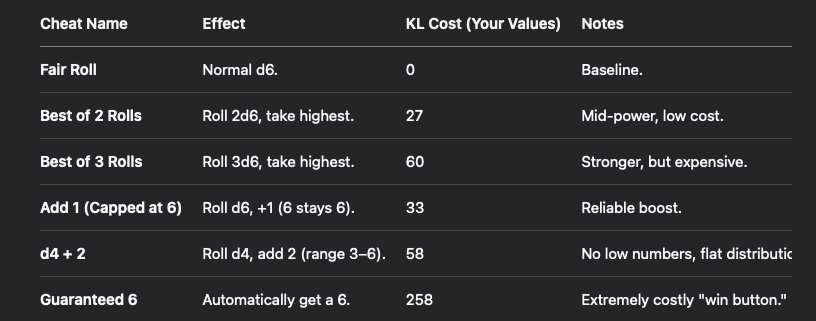
If you want to model "plausible luck" in a game you can make KL-divergence the resource. Here's the meta-rule you can apply to any game: give each player some "luck" at the start of the game, say 100. Any time they are about to roll (let's say d6) they're allowed to replace the uniform distribution with one of their choosing, but the price they pay will be 100 D(required distribution|uniform) (in bits).
Of course you don't make players calculate stuff. I've provided a convenient menu.
Choosing exactly 6 is expensive. Maybe they need to start with more points.
One interesting side effect of this is that if an observer is watching the die roll outcomes, but not the actual mechanics, it'll be hard to see that "luck" is being used.
There is, I think, some interesting non-trivial strategy for how best to use luck in any particular game. If the game is "get the highest sum of N dice" then you want to spread your luck out as much as possible.
(ChatGPT made the table but I did the computation myself.)
guile really needs a left-pad library, it's not vulnerable to a single point of failure enough
ﾇﾈﾏﾇﾃｨにいくぞ（ふとん）
If you are a foreign national, of any country, of any color, of any gender presentation, of any sexual preference, of any credentials, of any politics, I urge you to avoid my country, the United States.
We have secret police now, and they are convinced that they can do anything, to anyone, for any reason.
I never thought we'd have junior-league Stasi active here, but that is the situation.
Stay where you are, don't come here. It is not welcoming, and it is not even safe.
#FediForum premiere for my Fediverse promo film = done.
How did it go? So well that I've been fighting back tears for the past half hour.
Getting such warm, positive comments from builders and champions of the fediverse is EVERYTHING ❤️ Thank you 
@j12tJohannes Ernst for this opportunity.
I'm almost tempted to "deploy on a Friday" and share the link to the video now 😅 But nah, I know better. Tuesday it is! (Monday is a public holiday here)
Have a lovely weekend everyone!
PHSのはなししました！？ これは昔うちにあったのとは違うけど…（AirH"だった）
트위터의 새로운 암호화 DM은 이전 것보다 더 낫지 않음
------------------------------
- *Twitter(X)의 새 암호화 DM(XChat)* 은 * 기술적으로 end-to-end 암호화*를 표방하지만, * 프라이빗 키 탈취·MITM·메타데이터 노출 등 심각한 보안 결함*이 여전히 존재함
- *Libsodium Box(비밀키 기반 암호화)** 를 도입했으나, * forward secrecy 미지원*과 4자리 PIN 기반 약한 키 보호 방식으로 * 프라이…
------------------------------
https://news.hada.io/topic?id=21324&utm_source=googlechat&utm_medium=bot&utm_campaign=1834
Newsom blasts deployment of National Guard to LA as 'purposefully inflammatory' (Melanie Mason/Politico)
https://www.politico.com/news/2025/06/07/newsom-national-guard-los-angeles-00393526
http://www.memeorandum.com/250607/p60#a250607p60
요즘 본격적인 바이브 코딩 말고 자잘한 수정은 그냥 Warp에서 에이전트 모드를 쓰고 있는데, 적당히 잘 굴러가서 괜찮다.
手動でいくぜ
#Fediverseプロフ帳 でプロフィールカードを作成しました！ #okprint https://purofu.y-zu.org/view/card?id=1264 #プロフ帳 #プロフィール帳
よっこいし 
Update `SafeReblogInsert` concern to match Rails 8 method (#34966)
Add `fasp` queue to sidekiq queue system check (#34965)
Change github workflow for chromatic to only run on official Mastodon repository (#34963)
fix: Fix indentation of quote posts in threads (#34961)
fix: update search column input on param change (#34951)
Update `rack` to 3.1.16 (#34959)
Rewrite `AccountNote` as Typescript functional component (#34925)
feat: Add Storybook for component documentation, testing, and development (#34907)
Remove `inbound_quotes` feature flag (#34958)
Align versions in templates to current/plausible values (#34952)
Fix quote post streaming edge cases (#34957)
New Crowdin Translations (automated) (#34953)
fix(deps): update dependency postcss-preset-env to v10.2.1 (#34947)
chore(deps): update dependency ruby-vips to v2.2.4 (#34949)
Add ability to filter quote posts in home timeline (#34946)
Change “legacy” non-fast-tracked quote posts to not be displayed as such (#34945)
続
できた？
在我出門的時候還沒有預期今天會騎到東港的，
可能是那海在呼喚我吧！
每次會覺得自己從日本回到了香港的一刻：在家裡聽見外面的路人在說廣東話
12 4 
: 4
Writing a good blog post is surprisingly difficult. I'm now 3+ hours in, and my initial blog post was almost 20 minutes long, the latest version is a 5-min read.
"If I Had More Time, I Would Have Written a Shorter Letter"
「もう今の時代はAIで◯◯できちゃうからさー」って言ってる人に「え、そうなんすか。じゃあ今それやってみてくださいよ」っていうと、だいたいできない。
Joining Apple Computer
Link: https://www.folklore.org/Joining_Apple_Computer.html
Discussion: https://news.ycombinator.com/item?id=44212441
「もう今の時代はAIで◯◯できちゃうからさー」って言ってる人に「え、そうなんすか。じゃあ今それやってみてくださいよ」っていうと、だいたいできない。
GENKI
Evan Prodromou
@reiver ⊼ (Charles) 
sublimer@あすてろいどん鯖管
Emelia 👸🏻
Juntai Park
