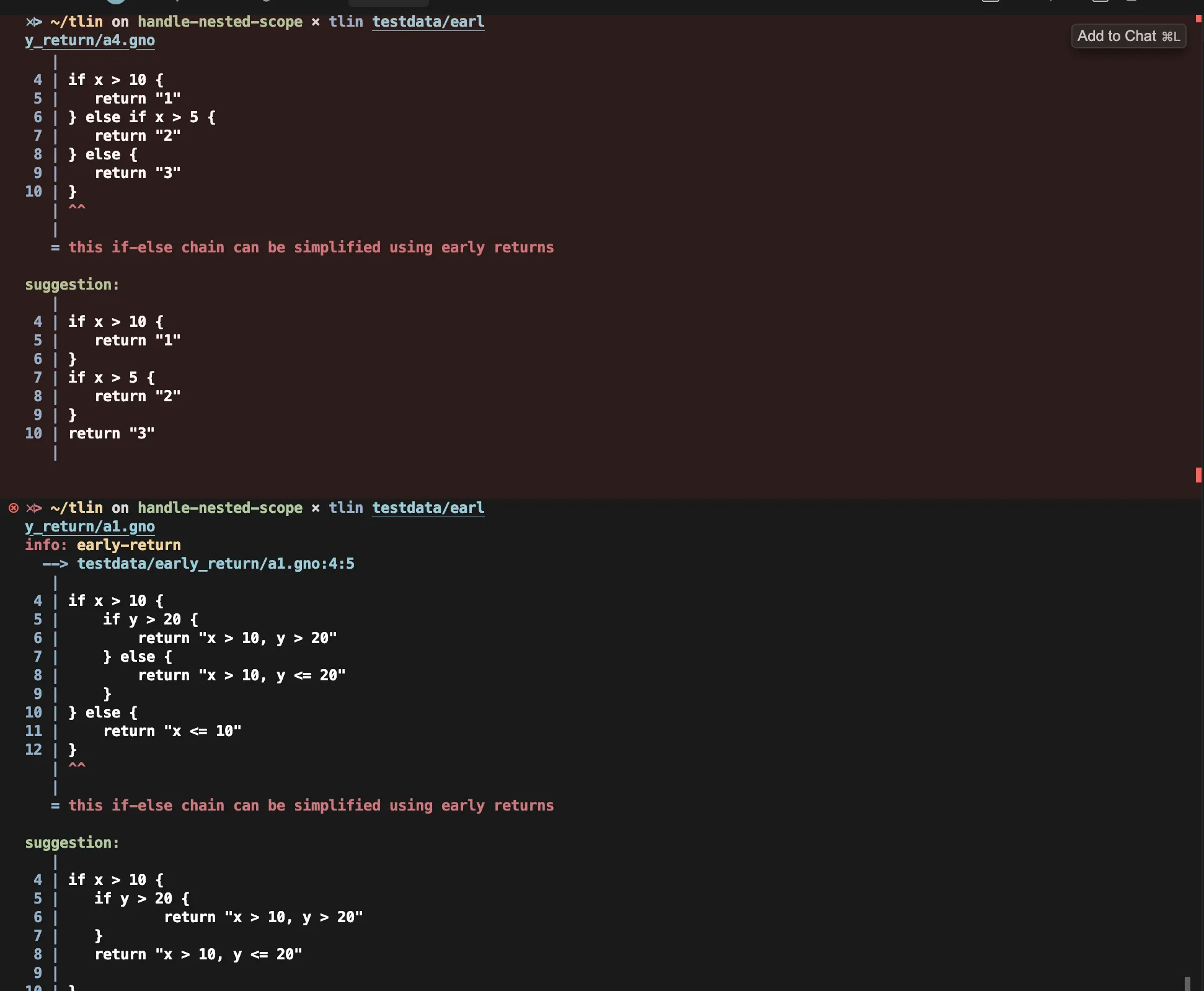
러스트를 너무 안만졌더니 슬슬 다시 가뭏가물하다
notJoon
@joonnot@hackers.pub · 52 following · 64 followers
Uncertified Quasi-pseudo dev
와, 이거 진짜 짱이다 cc @joonnotnotJoon
와, 이거 진짜 짱이다 cc @joonnotnotJoon
이래서 금요일엔 배포하는거 아니다
해결
한시간 전까지는 잘 돌아가던 배포 스크립트가 갑자기 실행이 안되는 건에 대하여
이래서 금요일엔 배포하는거 아니다
한시간 전까지는 잘 돌아가던 배포 스크립트가 갑자기 실행이 안되는 건에 대하여
회사 슬랙에 읽을만한 글을 공유하고 있는데 한 몇번 하니까 참여도가 상당히 올라왔다. 원래 농땡이 칠겸 시작했던건데 결과는 좋은걸로
notJoon shared the below article:
웹 접근성이 UI 설계에 중요한 이유
김무훈 @iamuhun@hackers.pub
웹 접근성의 중요성과 WAI-ARIA 표준을 바탕으로 한 의미론적인 UI를 설계한 사례를 블로그에 공개했습니다.
전문성 검증이 필요한 분야이다 보니, 퇴고 과정에 접근성 전문가 @resistan 님의 도움을 받았습니다.
타입스크립트를 깊게 파보지는 않아서 쓸 때마다 뭔가 아쉽다. 날 잡고 폐관수련 해야할듯
언젠가 읽어야지 하다가 이제야 샀다
확실히 문서에 잘 정리해놓으니까 AI랑 협업하기가 수월한 것 같음. 개인 프로젝트에도 잘 해놓으면 아주 좋겠구먼
@joonnotnotJoon CONTRIBUTING.md 파일 하나 잘 작성해 두면 사람이랑 협업할 때 뿐만 아니라 LLM이랑 협업할 때도 도움이 많이 되더라고요. Hackers' Pub도 하나 마련해 뒀어요.
@joonnotnotJoon CONTRIBUTING.md 파일 하나 잘 작성해 두면 사람이랑 협업할 때 뿐만 아니라 LLM이랑 협업할 때도 도움이 많이 되더라고요. Hackers' Pub도 하나 마련해 뒀어요.
![]() @hongminhee洪 民憙 (Hong Minhee) 오늘 해커스펍 레포 보면서 많이 배워갔습니다 👍
@hongminhee洪 民憙 (Hong Minhee) 오늘 해커스펍 레포 보면서 많이 배워갔습니다 👍
확실히 문서에 잘 정리해놓으니까 AI랑 협업하기가 수월한 것 같음. 개인 프로젝트에도 잘 해놓으면 아주 좋겠구먼
@joonnotnotJoon Use Repomix
cursor로 문서와 터미널을 연동시키니까 환경 세팅 할 때의 고통이 줄어들었다
확실히 문서에 잘 정리해놓으니까 AI랑 협업하기가 수월한 것 같음. 개인 프로젝트에도 잘 해놓으면 아주 좋겠구먼
cursor로 문서와 터미널을 연동시키니까 환경 세팅 할 때의 고통이 줄어들었다
...구글은 사업 접어라
notJoon shared the below article:
함수형 언어의 평가와 선택
Ailrun (UTC-5/-4) @ailrun@hackers.pub
함수형 언어(Functional Language)의 핵심
함수형 언어가 점점 많은 매체에 노출되고, 더 많은 언어들이 함수형 언어의 특징을 하나 둘 받아들이고 있다. 함수형 언어, 적어도 그 특징이 점점 대세가 되고 있다는 이야기이다. 하지만, 함수형 언어가 대체 무엇이란 말인가? 무엇인지도 모르는 것이 대세가 된다고 할 수는 없지 않은가?
함수형 언어란 아주 단순히 말해서 함수가 표현식[1]인 언어를 말한다. 다른 말로는 함수가 값이기 때문에 다른 함수를 호출해서 함수를 얻어내거나 함수의 인자로 함수를 넘길 수 있는 언어를 말한다. 그렇다면 이 단순화된 핵심만을 포함하는 언어로 함수형 언어의 핵심을 이해할 수 있지 않을까? 이게 바로 람다 대수(Lambda Calculus)의 역할이다.[2]
람다 대수는 딱 세 종류의 표현식만을 가지고 있다.
- 변수 (xx, yy, …\ldots)
- 매개변수 xx에 인자를 받아 한 표현식 MM(함수의 몸체)을 계산하는 함수 (λx→M\lambda x\to M)
- 어떤 표현식 LL의 결과 함수를 인자 NN으로 호출 (L NL\ N)
이후의 설명에서는 MM 과 NN, 그리고 LL이라는 이름을 임의의 표현식을 나타내기 위해 사용할 것이다. 람다 대수가 어떤 것들을 표현할 수 있는가? 앞에서 말했듯이 람다 대수는 함수의 인자와 함수 호출의 결과가 모두 함수인 표현식을 포함한다. 예를 들어 λx→(λy→y)\lambda x \to (\lambda y \to y) 는 매개변수 xx에 인자를 받아 함수 λy→y\lambda y \to y를 되돌려주는 함수이고, λx→(x (λy→y))\lambda x \to (x\ (\lambda y \to y))는 매개변수 xx에 함수인 인자를 받아 그 함수를 (λy→y\lambda y \to y를 인자로 사용하여) 호출하는 함수이다.
람다 대수(Lambda Calculus)의 평가(Evaluation)
이제 문제는
그래서 람다 대수의 표현식이 하는 일이 뭔데?
이다. 위의 표현식에 대한 소개는 산수로 말하자면 x+yx + y와 같이 연산자(++)와 연산항(xx와 yy)로부터 얻어지는 문법만을 설명하고 있고, 3+53 + 5와 같은 구체적인 표현식을 계산해서 88이라는 결과 값을 내놓는 방식을 설명하고 있지 않다. 이런 표현식으로부터 값을 얻어내는 것을 언어의 "평가 절차"("Evaluation Procedure")라고 한다. 람다 대수의 평가 절차를 설명하는 것은 어렵지 않다. 적어도 표면적으로는 말이다.
- 함수는 이미 값이다.
- 함수 λx→M\lambda x \to M을 NN으로 호출하면 MM에 등장하는 모든 xx을 NN으로 치환(Substitute)하고 결과 표현식의 평가를 계속한다.
이는 겉으로 보기에는 말이 되는 설명처럼 보인다. 하지만 이 설명을 실제로 해석기(Interpreter)로 구현하려고 시도한다면 이 설명이 사실 여러 세부사항을 무시하고 있다는 점을 깨닫게 될 것이다.
- 함수 호출 L NL\ N에서 LL이 (아직) λx→M\lambda x \to M 꼴이 아닐 때는 어떻게 해야하지?
- 함수 호출 (λx→M) N(\lambda x \to M)\ N에서 NN을 먼저 평가하는 게 낫지 않나? xx가 MM에 여러번 등장한다면 NN을 여러번 평가해야 할텐데?
첫번째 문제는 비교적 간단히 해결할 수 있다. LL을 먼저 평가해서 λx→M\lambda x \to M 꼴의 결과 값을 얻어낸 뒤에 호출을 실행하면 되기 때문이다. 반면에 두번째 질문은 좀 더 미묘한 문제를 가지고 있다. 함수 호출의 평가에서 발생하는 이 문제에 구체적인 답을 하기 위해서는 값에 의한 호출(Call-By-Value, CBV)와 이름에 의한 호출(Call-By-Name, CBN)이 무엇인지 이해해야 한다.
값에 의한 호출(Call-By-Value)? 이름에 의한 호출(Call-By-Name)?
앞에서 말한 함수 호출에서부터 발생하는 문제는 사실 함수형 언어에서만 발생하는 문제는 아니다. C와 같은 명령형 언어에서도 함수를 호출할 때 인자를 먼저 평가해야하는지를 결정해야하기 때문이다. 즉 이 문제는 함수를 가지고 있고 함수를 호출해야하는 모든 언어들이 가지고 있는 문제이다.
그렇다면 이 일반적인 문제를 어떻게 해결하는가? 대부분의 언어가 취하는 가장 대표적인 방식은 "값에 의한 호출"("Call-By-Value", "CBV")이라고 한다. 이 함수 호출 평가 절차에서는 함수의 몸체에 인자를 치환하기 전에[3] 인자를 먼저 평가한다. 이 방식을 사용하면 인자를 여러번 평가해야하는 상황을 피할 수 있다.
또 다른 방식은 "이름에 의한 호출"("Call-By-Name", "CBN")이라고 한다. 이 방식에서는 함수의 몸체에 인자를 우선 치환한 후 몸체를 평가한다. 몇몇 언어의 매크로(Macro)와 같은 기능이 이 방식을 사용한다. 얼핏 보기에는 CBN은 장점이 없어보인다. 그러나 함수가 인자를 사용하지 않을 경우는 CBN이 장점을 가진다는 것을 볼 수 있다. 극단적으로 평가가 종료되지 않는 표현식(Non-terminating expression)이 있다면[4] CBV는 종료하지 않고 CBN만이 종료하는 경우가 있음을 다음 예시를 통해 살펴보자. 표현식 (λx→(λy→y)) N(\lambda x \to (\lambda y \to y))\ N이 있다고 할 때, NN이 평가가 종료되지 않는 표현식이라고 하자. 이 경우 CBV를 따른다면 종료하지 않는 NN 평가를 먼저 수행하느라 이 표현식의 값을 얻어낼 수 없지만, CBN을 따른다면 λy→y\lambda y \to y라는 값을 손쉽게 얻어낼 수 있다. 바로 이런 상황 때문에
CBN은 CBV보다 일반적으로 더 많은 표현식들을 평가할 수 있다
고 말한다.
모호한 선택을 피하는 방법
두 방식의 장점을 모두 가질 수는 없을까? 다시 말해서, 어떤 상황에서는 이름에 의한 호출을 사용하고, 어떤 상황에서는 값에 의한 호출을 사용할 수 없을까? 이 질문에 답한 수많은 선구자들 가운데 폴 블레인 레비(Paul Blain Levy)가 내놓은 답인 "값 밀기에 의한 호출"("Call-By-Push-Value", "CBPV")은 함수형 언어의 평가를 기계 수준(Machine level)에서 이해하는데에 있어 강력한 도구를 제공한다. CBPV는 우선 "계산"("Computation")과 "값"("Value")을 구분한다.
- 계산 MM, NN, LL, …\ldots = 함수 λx→M\lambda x \to M 또는 함수 호출 L VL\ V
- 값 VV, UU, WW, …\ldots = 변수 xx
잠깐, 앞서서 함수형 언어에서 함수는 값이라고 하지 않았던가? 이는 값 밀기에 의한 호출에서 함수와 함수 호출을 종전과 전혀 다르게 이해하기 때문이다. 함수 λx→M\lambda x \to M는 스택(Stack)에서 값을 빼내어(Pop) xx라는 이름을 붙인 후 MM을 평가하는 것이고, 함수 호출 L VL\ V는 스택에 값 VV를 밀어넣고(Push)[5] LL을 평가하는 것이다. 따라서 함수 λx→M\lambda x \to M는 평가의 결과가 아닌 추가적인 평가가 가능한 표현식이 된다. 이 구분을 간결하게 설명하는 것이 다음의 CBPV 표어이다.
값은 "~인 것"이다. 계산은 "~하는 것"이다.
그렇지만 함수형 언어이기 위해서는 함수를 값으로 취급할 수 있어야 한다고 했지 않은가? 그렇다. 이를 위해 CBPV는
계산을 강제한다면(force\mathbf{force}) 계산 MM를 하는 지연된 계산인 값 thunk(M)\mathbf{thunk}(M)
을 추가로 제공한다. 이 둘 (force(V)\mathbf{force}(V)와 thunk(M)\mathbf{thunk}(M))을 다음과 같이 문법에 추가할 수 있다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V)
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
CBPV를 완성하기 위해 필요한 마지막 조각은 계산을 끝내는 법이다. 현재까지 설명한 λx→M\lambda x \to M와 L VL\ V 그리고 force(V)\mathbf{force}(V) 는 모두 다음 계산을 이어서 하는 표현식이고, 계산을 끝내는 방법을 제공하지는 않는다. 예를 들어 λx→M\lambda x \to M의 평가는 스택에서 값을 빼내고 계산 MM의 평가를 이어한다. 그렇다면 계산의 끝은 무엇인가? 결과 값을 제공하는 것이다. 이를 위해 return(V)\mathbf{return}(V)를 계산에 추가하고, 이 결과 값을 사용할 수 있도록 M to x→NM\ \mathbf{to}\ x \to N (계산 MM을 평가한 결과 값을 xx라고 할 때 계산 NN을 평가하는 계산) 또한 계산에 추가하면 다음의 완성된 CBPV를 얻는다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V) 또는 return(V)\mathbf{return}(V) 또는 M to x→NM\ \mathtt{\mathbf{to}}\ x \to N
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
이제 CBPV를 얻었으니 원래의 목표로 돌아가보자. 어떻게 CBV 호출과 CBN 호출을 CBPV로 설명할 수 있을까?
- CBV 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 return(thunk(λx→M))\mathbf{return}{(\mathbf{thunk}(\lambda x \to M))}과 L to x→N to y→force(x) yL\ \mathbf{to}\ x \to N\ \mathbf{to}\ y \to \mathbf{force}(x)\ y로 표현할 수 있다. 즉, CBPV의 관점에서 CBV의 함수는 지연된 원래 계산 λx→M\lambda x \to M을 값으로 되돌려주는 계산으로 이해할 수 있고, 함수 호출 L NL\ N은 함수 부분 LL을 먼저 평가하고 NN을 평가한 뒤 NN의 계산 결과 yy를 스택에 밀어넣고 지연된 계산인 함수 부분 xx의 계산을 강제하는(force(x)\mathbf{force}(x)) 것으로 이해할 수 있다.
- CBN 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 λx→M\lambda x \to M(단, 변수 xx의 모든 사용을 force(x)\mathbf{force}(x)로 치환함)과 L thunk(N)L\ \mathbf{thunk}(N)로 표현할 수 있다. 즉, CBPV의 관점에서 함수 호출은 L NL\ N은 지연된 NN을 스택에 밀어넣은 뒤 LL의 계산을 이어가는 것으로 볼 수 있다. 이 지연된 NN은 이후에 스택에서 빼내어져 어떤 이름 xx가 붙은 뒤, 이 변수가 사용될 때에야 비로소 계산된다.
다소 설명이 복잡할 수 있으나, 단순하게 말해서 CBPV는 CBV에 따른 상세한 평가 순서와 CBN 따른 상세한 평가 순서를 세부적으로 설명할 수 있는 충분한 기능을 모두 갖추고 있으며, 이를 통해 CBV 함수 호출과 CBN 함수 호출을 모두 설명할 수 있다는 이야기이다.
기계 수준(Machine level)에서의 Call-By-Push-Value의 장점
앞에서는 CBPV가 CBV와 CBN를 모두 설명할 수 있음을 다뤘다. 그러나 CBPV는 프로그래머(Programmer)가 직접 사용하기에는 과도하게 자세한 세부사항들을 포함하고 있기에, 프로그래머가 직접 CBPV를 써서 CBV와 CBN의 구분을 조율하기에는 적합하지 않다. 그렇다면 어느 수준에서 CBV와 CBN을 혼합해 사용할 때 도움을 줄 수 있을까? 바로 람다 대수를 기계 수준으로 컴파일(Compile)할 때이다. 이때는 CBPV가 가진 자세한 세부사항의 표현력이 굉장히 유용해진다.
예를 들어 람다 대수를 기계 수준으로 변환할 때 흔히 필요한 것 중 하나인 항수 분석(Arity analysis)에 대해 이야기해보자. 항수 분석은 함수가 하나의 인자를 받은 뒤 실행되어야 하는지, 혹은 두 인자를 모두 받아 실행되어야 하는지 등을 확인하여 이후에 그에 걸맞는 최적화된 기계어(Machine language)를 생성할 수 있게 도와주는 분석 작업이다. 평범한 람다 대수에서는 항수 분석의 결과를 직접적으로 표현하기 어렵다. 예를 들어 람다 대수의 λx→(λy→y)\lambda x \to (\lambda y \to y)의 경우 이 함수가 xx와 yy를 모두 받아 yy를 되돌려주는 함수인지 (항수가 2인 함수인지), 혹은 xx를 받아 λy→y\lambda y \to y라는 함수를 되돌려주는 함수인지 (항수가 1인 함수인지) 구분할 수 없다. 그러나 이를 CBPV로 변환한 λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))나 λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 각각이 무엇을 뜻하는지 분명히 이해할 수 있다.
- λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))는 두 변수 xx와 yy를 스택에서 빼낸 뒤 yy의 값을 되돌려주는 함수(항수가 2인 함수)이다.
- λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 변수 xx를 스택에서 빼낸 뒤 지연된 계산 λy→return(y)\lambda y \to \mathtt{return}(y)를 돌려주는 함수(항수가 1인 함수)이다.
이런 장점을 바탕으로 CBPV를 더 발전시킨 "언박싱한 값에 의한 호출"("Call-By-Unboxed-Value")을 GHC 컴파일러의 중간 언어(Intermediate language)로 구현하는 것에 대한 논의가 현재 진행되고 있으며 앞으로 더 많은 함수형 컴파일러들이 관련된 중간 언어를 채용하기 시작할 것으로 보인다.
마치며
이 글에서는 함수형 언어의 핵인 람다 대수를 간단히 설명하고 람다 대수를 평가하는 방법에 대해서 다루어보았다. 특히 그 중 값 밀기에 의한 평가(Call-By-Push-Value, CBPV)가 무엇이며 CBPV가 다른 대표적인 두 방법(CBV, CBN)을 어떻게 표현할 수 있는지, 그리고 CBPV의 장점이 무엇인지에 대해서도 다루어 보았다. 이 글에서 미처 다루지 못한 중요한 주제는 CBPV를 기계에 가까운 언어로 번역해보는 것이다. 여기에서는 글이 너무 복잡해지는 것을 피하기 위해 제했으나, CBPV의 장점에서 살펴봤듯 이는 CBPV에 있어 핵심 주제 중 하나이기 때문에 이후에 다른 글을 통해서라도 이 주제를 소개할 기회를 가지고자 한다. 이 글이 CBPV에 대한 친절한 소개글이었기를 바라며 이만 줄이도록 하겠다.
결과 값(Value)을 가지는 언어 표현을 말한다. 예를 들어 1+11 + 1은 22라는 값을 가지는 표현식이지만 (JavaScript의)
let x = 3;나 (Python의)def f(): ...은 그 자체로는 값이 없기 때문에 표현식이 아니다. ↩︎다만 실제 역사에서는 람다 대수의 이해와 발견이 함수형 언어의 개발보다 먼저 이루어졌다. 이런 역사적 관점에서는 (이미 많은 수학자들이 이해하고 있던) 람다 대수에 여러 기능을 추가한 것이 바로 함수형 언어라고 볼 수 있다. ↩︎
프로그래밍 언어(Programming Language)는 실제로는 치환을 사용하지 않고 환경(Environment)을 사용하는 경우가 더 많지만 설명의 편의를 위해 다른 언어들 또한 환경 대신 치환에 기반해 평가한다고 가정하겠다. ↩︎
앞서 설명한 람다 대수에서는 이를 쉽게 얻을 수 있다. 오메가(Ω\Omega)라고 부르는 표현식인 (λx→x x) (λx→x x)(\lambda x \to x\ x)\ (\lambda x \to x\ x)의 평가는 값에 의한 호출을 따르든 이름에 의한 호출을 따르든 종료되지 않는다. ↩︎
바로 이 함수 호출을 값 밀기에 기반해 해석하는 데에서 CBPV의 이름이 유래했다. ↩︎
이전에 CFG로 AST의 동등성을 비교하는 기능을 구현했었는데, 정직하게 구조로만 분석하다보니까 동등한 semantic이여도 구조가 달라지면 인식을 못하는 사소한 문제가 있구먼
https://github.com/gnolang/gno/pull/4174 오늘은 입출력 패키지의 최적화 작업을 했다. 아직까지는 벤치마크를 찍어볼 수 없어서 간접적인 정보로만 성능 향상이 이루어졌음을 확인해야 한다는게 좀 아쉽지만, 그래도 만족스러운 결과다.
역시 파서나 문자열 다루는게 가장 재밌음
CFG 경로 구조 분석할 때 trie 쓰니까 성능이 괜찮아졌다
2025年 오픈소스 컨트리뷰션 아카데미 參與型 멘토團 募集 公告가 떴다. Fedify 프로젝트의 메인테이너로서 멘토團에 志願하고자 한다. 志願書가 .hwp 파일이기에 큰 맘 먹고 한컴오피스 한글 for Mac도 購入했다. (아무래도 앞으로 .hwp 파일 다룰 일이 많을 것 같다는 豫感이 들어서…)
자동 수정 반영 전에 리팩토링된 코드가 이전과 동일한지 검증하는 기능을 일단 CFG를 이용해서 구현해봐야겠다.
notJoon shared the below article:
같은 것을 알아내는 방법
Ailrun (UTC-5/-4) @ailrun@hackers.pub
이 글은 일상적인 질문에서부터 컴퓨터 과학의 핵심 문제에 이르기까지, '같음'이라는 개념이 어떻게 적용되고 해석되는지를 탐구합니다. 특히, 두 프로그램이 '같은지'를 판정하는 문제에 초점을 맞춰, 문법적 비교와 $\beta$ 동등성이라는 두 가지 접근 방식을 소개합니다. 문법적 비교는 단순하지만 제한적이며, $\beta$ 동등성은 프로그램의 실행을 고려하지만, 계산 복잡성으로 인해 적용이 어렵습니다. 이러한 어려움에도 불구하고, 의존 형 이론에서의 형 검사(변환 검사)는 $\beta$ 동등성이 유용하게 활용될 수 있는 중요한 사례임을 설명합니다. 이 글은 '같음'의 개념이 프로그래밍과 타입 이론에서 어떻게 중요한 역할을 하는지, 그리고 이 개념을 올바르게 이해하고 구현하는 것이 왜 중요한지를 강조하며 마무리됩니다.
Read more →오랜기간 나를 괴롭혔던 불필요한 else문 제거 기능이 드디어 잘 동작한다.
notJoon shared the below article:
Hacker's Pub에 입문한 한국어권 여러분을 위한 안내서
Jaeyeol Lee @kodingwarrior@hackers.pub
Hacker's Pub은 소프트웨어 업계 종사자들이 자유롭게 생각을 공유하고 소통할 수 있는 소셜 네트워크 서비스이자 블로깅 플랫폼입니다. ActivityPub 프로토콜을 지원하여 Mastodon, Misskey 등 다른 SNS 서비스 사용자들과도 연결되어 플랫폼 경계를 초월한 소통이 가능합니다. 이 글에서는 Hacker's Pub의 의미와 ActivityPub 프로토콜에 대한 간략한 소개, 그리고 커뮤니티에 기여할 수 있는 다양한 방법을 제시합니다. 오픈 소스로 개발되는 Hacker's Pub 생태계에 참여하여 함께 서비스를 발전시키고, 우리만의 클라이언트를 만들어 Hashnode와 같은 블로그 템플릿을 구축하는 미래를 기대해 볼 수 있습니다. Hacker's Pub은 상호 존중과 신뢰를 바탕으로 모든 이들이 자유롭게 의견을 나누고 함께 만들어가는 공간입니다.
Read more →버그의 입장에서 보면, 개발자가 하는 일이란 하나의 커다란 버그를 여러개의 작은 버그들로 끝없이 바꾸는 작업이다. 언제까지? 사용자 눈에 띄지 않을 때까지.
hello world
@joonnotnotJoon 여기서 반가워요
![]() @kodingwarriorJaeyeol Lee 여기가 바로 원피스군요
@kodingwarriorJaeyeol Lee 여기가 바로 원피스군요