台湾のg0v summit 2026の早割チケットが明日3/3の現地時間10時から販売開始らしい。
シビックテックを最近知った、かつ内向的な人間が個人としていきなり海外カンファレンスに参加するのは勇気がいるけど、もうチケット買っちゃって退路を塞ごうかな…!
https://g0v.social/@summit/116157874383012918
洪 民憙 (Hong Minhee)
@hongminhee@hackers.pub · 1016 following · 722 followers
Hi, I'm who's behind Fedify, Hollo, BotKit, and this website, Hackers' Pub! My main account is at ![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)  .
.
Fedify, Hollo, BotKit, 그리고 보고 계신 이 사이트 Hackers' Pub을 만들고 있습니다. 제 메인 계정은: ![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)  .
.
Fedify、Hollo、BotKit、そしてこのサイト、Hackers' Pubを作っています。私のメインアカウントは「![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)  」に。
」に。
Website
- hongminhee.org
GitHub
- @dahlia
Hollo
- @hongminhee@hollo.social
DEV
- @hongminhee
velog
- @hongminhee
Qiita
- @hongminhee
Zenn
- @hongminhee
Matrix
- @hongminhee:matrix.org
X
- @hongminhee
코딩하다가 막혀서 클로드한테 물어보려고 프롬프트를 짜고 있으면 문득 뭐가 문제인지 보여서 쓰던 프롬프트를 버리고 그냥 인간지능으로 고치는 일이 자주 생긴다...
ㄴ 너 방금 러버덕 디버깅을 발명했어
그 뭐시냐.... 제가 모임 개최 플랫폼 (대충 https://event-us.kr 혹은 https://connpass.com 같은거) + 지역 기반 리뷰 서비스 (대충 포스퀘어 같은거) 를 만들었는데요.
**당연히, 연합우주 거주민 대상으로 만들어진 서비스이고, 연합우주에 계정이 있다면 누구나 OTP 로그인으로 인증이 가능합니다**
어떻게 만들어나갈지 나름 고민은 많이 해봤고, 내가 생각하는 고민이랑 다른 사람들이 생각하는 수요가 일치하는지 확인도 하고 싶어서 이렇게 공개적인 글을 올립니다.
많은 관심과 사랑 부탁드리고, 문의사항이나 피드백 있으면 GitHub Issue로 부탁드리겠습니다. GitHub 링크 : https://github.com/moim-social/moim
물론, 다른 창구도 열어둘 여지는 있습니다. 디스코드 채널은.. 당장은 https://fedidev.kr 의 #moim 채널을 이용하지 않을까 싶구요.
오랜만입니다. 근황 겸...
2월 말 퇴사했습니다. 역시 Web3는 제가 "잘" 하는거지 "좋아" 하진 않는 것 같습니다. 평가도 좋고 계속 할 수도 있었지만 뭔가 이젠 시들해지기도 했고, 원래부터 Web3로 커리어를 잡으려고 했던 것도 아니라서 다음 직장을 알아봤습니다.
그래서 4월 1일부터 크레페(쿠키플레이스)로 옮깁니다. 김민상(bis_cir_kit) 님 추천으로 지원하게 되었는데, 타입으로 그래프 나타내는 건 원래 좋아하던 일이라서 스택도 잘 맞고, 회사 감성도 완전 찰떡이라 일주일 만에 합류 결정이 되었습니다.
그 사이엔 결혼 일정때문에 바빴습니다. 3월 7일에 대구에서 결혼합니다. 너무 멀어서 미안한 나머지 청첩장은 많이 못 돌렸지만 이렇게나마 소식은 전합니다.
wedding.suho.io 에서 저희 사진과 정보를 더 확인하실 수 있습니다.
또한 2월 중순쯤 퇴사가 확정되고 나서 만들고 있는 프로젝트가 있습니다. whaleback.suho.io 입니다. 한국 주식을 각 종목별로 퀀트 분석해 주고, AI 리포트로 일간 트렌드를 알려주는 등, 각종 정보를 보기 편하게 정리했습니다.
사용해 보시고 궁금한 점 있거나, 아니면 저 개인이 궁금하시더라도 연락주세요. 감사합니다.
AI 에이전트의 신뢰성 측정 방법을 제안하는 연구. 기존 에이전트 벤치마크가 평균 성공률에만 치중했기 때문에 평가 결과가 좋아도 실제 환경에서는 자주 실패함을 지적한다. 에이전트가 얼마나 일관되게 동작하는지, 환경 변화에 얼마나 버티는지, 실패를 예측할 수 있는지, 오류가 얼마나 심각한지 알기 위해서는 정확성이 아닌 신뢰성을 평가해야 한다는 것이다. https://hal.cs.princeton.edu/reliability/
ChatGPT가 한국어로 "너 **핵심을 찔렀어"같이 말하는 것처럼 일본어에선 結論から言うと(결론부터 말하자면)로 시작하는 경우가 많다고 한다.
그리고 지금 내 Codex 세션이 딱 그런 느낌으로 응답하고 있네...
오늘 하루 Hackers Pub iOS 앱에 작업한 것들
- 긴 글을 잘라서 보여줄 때 HTML truncate할 때 HTML 태그 구조에 이상이 없게끔 안전하게 처리
- 글 리스트 보여줄 때 렌더링 최적화
- 글 리스트 / 상세 페이지에서 인용된 글도 제대로 보이도록 수정하고 인용 기능 추가
- 글에 반응하기 기능 추가
- 누가 글을 공유하거나 인용했는지 화면 추가
조금만 더 하면... 앱스토어 올려도 되겠다...
I've been saying for a while that we need something like FediCon in East Asia. A dedicated conference is still a stretch, but I've been thinking about a smaller step:
![]() @COSCUP 2026 (Taipei, Aug 8–9) is accepting proposals for community tracks. It might be worth trying to open a Social Web track there—something in the spirit of the Social Web devroom at FOSDEM.
@COSCUP 2026 (Taipei, Aug 8–9) is accepting proposals for community tracks. It might be worth trying to open a Social Web track there—something in the spirit of the Social Web devroom at FOSDEM.
Nothing is decided yet, but if you're working on #ActivityPub, the #fediverse, or anything in the social web space and might be interested in speaking (or co-organizing), I'd love to hear from you.
東아시아에도 FediCon 같은 行事가 있으면 좋겠다는 말을 여러 番 해왔는데요. 獨立的인 컨퍼런스는 아직 어렵더라도, 작은 첫걸음으로 생각해보고 있는 게 있습니다.
![]() @COSCUP 2026(臺北, 8月 8日–9日)이 커뮤니티 트랙 提案을 받고 있어요. FOSDEM의 Social Web devroom 같은 느낌으로, 거기서 Social Web 트랙을 열 수 있지 않을까 하고 構想 중입니다.
@COSCUP 2026(臺北, 8月 8日–9日)이 커뮤니티 트랙 提案을 받고 있어요. FOSDEM의 Social Web devroom 같은 느낌으로, 거기서 Social Web 트랙을 열 수 있지 않을까 하고 構想 중입니다.
아직 確定된 건 아무것도 없지만, #ActivityPub, #聯合宇宙, 或은 소셜 웹 全般을 다루고 있고 發表나 共同 오거나이징에 關心이 있으신 분이 있다면 이야기 걸어주세요.
I would like to migrate some of my projects to Codeberg, but since Codeberg doesn't seem to support PyPI's Trusted Publishing (yet), I don't think I'll be able to do that...
🚀 COSCUP 2026 Call for Participation is now open!
🎤 Community Tracks – Run a open-source agenda with talks, panels, or workshops. Apply by Mar 23. Spots are limited.
🛠 Community Booths – Showcase your project, recruit members, and connect. Apply by Jun 9. First come, first served.
👉 Apply here: https://s.coscup.org/26communityen
스택오버플로우 로고 이상해졌어
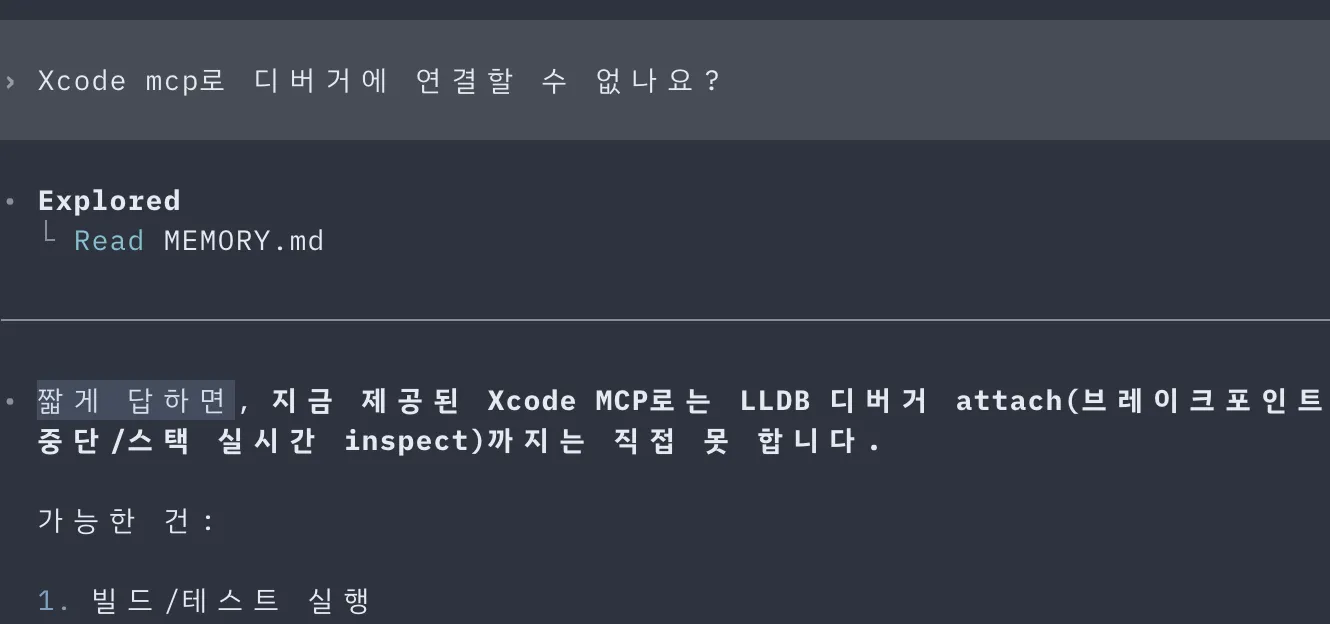
아... Emacs 정도의 확장성에 Zed 정도의 성능에 VS Code 정도의 까리함을 모두 갖는 에디터 어디 없나...
튜링의사과 오픈런하러감 끼얏호우~
개발자로서 느끼는 Nix의 최대장점은 패키지가 가능한한 최대로 configurable하다는 것이다. 가령 nixpkgs와 homebrew에 똑같이 10만개의 패키지가 있다고 하자. 하지만 nixpkgs에는 실제로 그보다 훨씬 많은 수의 패키지가 있는 셈이다. 저 10만개 외에도, 쉽게 설정을 바꿔서 안전하게 새로 빌드할수 있는 잠재적인 패키지들이 무수히 많기 때문이다.
요즘 일할 때 Opus 4.6보다 GPT-5.3 Codex를 애용하고 있지만 그럼에도 나는 Anthropic이 LLM의 alignment나 safety, explainability 분야에서 제일 잘 하고 있는 곳이라고 생각한다.
미국 정부와 관련된 일련의 사건에서 누가 잘잘못을 따지는 것과는 별개로 미국 정부가 저렇게까지 강경하게 나서서 가지지 못하면 부숴버리겠어!!!!!! 같은 스탠스를 취하고 있다는건, 그만큼 Anthropic의 모델이 우수해서가 아닐까.
그러고선 OpenAI가 Anthropic 자리를 대신 들어갔는데 정작 OpenAI도 Anthropic가 제한한걸 그대로 제한하고도 계약을 딴걸 보면 미국 정부가 자기네 정치적 이유로 OpenAI를 밀어줬거나 OpenAI는 미국 정부가 원하는 것을 이루기 위해 뒤에서 제한을 풀어주지 않을까하는 우려가 크다.
모델 선호에 대해 조금 더 말하자면 여전히 문서를 작성히거나 이미지가 필요 없는 모든 작업에선 Claude를 선호한다. 코딩 작업 시 planning과 review 단계에서 Codex를 훨씬 더 선호하고, 코드를 작성하거나 수정하는 일은 토큰 효율이나 시간 효율을 생각하면 Opus나 Sonnet이 더 좋다.
요즘 일할 때 Opus 4.6보다 GPT-5.3 Codex를 애용하고 있지만 그럼에도 나는 Anthropic이 LLM의 alignment나 safety, explainability 분야에서 제일 잘 하고 있는 곳이라고 생각한다.
미국 정부와 관련된 일련의 사건에서 누가 잘잘못을 따지는 것과는 별개로 미국 정부가 저렇게까지 강경하게 나서서 가지지 못하면 부숴버리겠어!!!!!! 같은 스탠스를 취하고 있다는건, 그만큼 Anthropic의 모델이 우수해서가 아닐까.
그러고선 OpenAI가 Anthropic 자리를 대신 들어갔는데 정작 OpenAI도 Anthropic가 제한한걸 그대로 제한하고도 계약을 딴걸 보면 미국 정부가 자기네 정치적 이유로 OpenAI를 밀어줬거나 OpenAI는 미국 정부가 원하는 것을 이루기 위해 뒤에서 제한을 풀어주지 않을까하는 우려가 크다.
Jiwon (![]() @z9mb1Jiwon), one of our core contributors, drew a Fedify dino! How cute!
@z9mb1Jiwon), one of our core contributors, drew a Fedify dino! How cute!
https://oeee.cafe/@z9mb1/2b5b0baf-466b-4c65-a1e0-d3588f0666f4
Fedify dino for notice
https://kre.pe/CKwN This is a paid request :) fediverse logo was attached afterwards.
@moim.liveMoim 를 해커스펍 못지않게 Fedify의 어지간한 기능을 지원하는 방향으로 개발하는 것이 목표....
2026년 튜링의 사과 할일
튜링의 사과 평일 SNS 모니터링 가동.
마스트돈에서도 꾸준히 활동 하기!
TIL: MDX를 쓸 때 <a href="https://example.com">테스트</a>처럼 태그 밖에 텍스트가 하나도 없으면 <p>로 감싸주지 않는다 (의도는 알겠는데 그래도 왜?)
Instead of using git as a database, what if you used database as a git?
I making auto-translated FEP document for Japanese, trying local models...
아오... gha버려야지 컨테이너 쓰는 경우 뭐 재사용 기능이 멀쩡한게 없네
beelink 미니PC를 주문했다. NixOS, Tvix, LLM 에이전트를 가지고 놀아보려고 한다.
[🍏매장안내]
튜링의 사과 키보드 타건 배치를 변경하였습니다.
브랜드별로 한쪽 공간에 배치하여 체험하실 수 있도록 구비 해놨습니다.
미니 해커톤, 무료 강연등 다양하고 알찬 프로그램 준비해보고자합니다. 언제든지 협업 문의가 있으시다면 연락주세요! 많은 관심 부탁드립니다.
튜링의 사과팀의 2026년 다양한 활동 기대해주세요!😄
日本かアジア圏でActivityPubとかオープンデータとかシビックテックのカンファレンスやイベントがあればちょっとずつ参加していきたいな。英語もまた話せるように鍛え直さないと…
シビックテックで取り組んでる課題をチームの皆で話してて、データはJSON-LDで記述したほうが良さそうとか、いずれシェア機能が欲しいねとか、コンテンツはオープンデータ化を前提としてデータの帰属は市民や地域コミュニティとしたいね等々を話し合う中で、「なんか…ActivityPub感…」と思った。
ActivityPubをオープンデータの流通・蓄積・活用の際に用いている取り組みとかって、あるのかな?
Open GLAMなどでありそうな気もするけど、どうなんだろ。
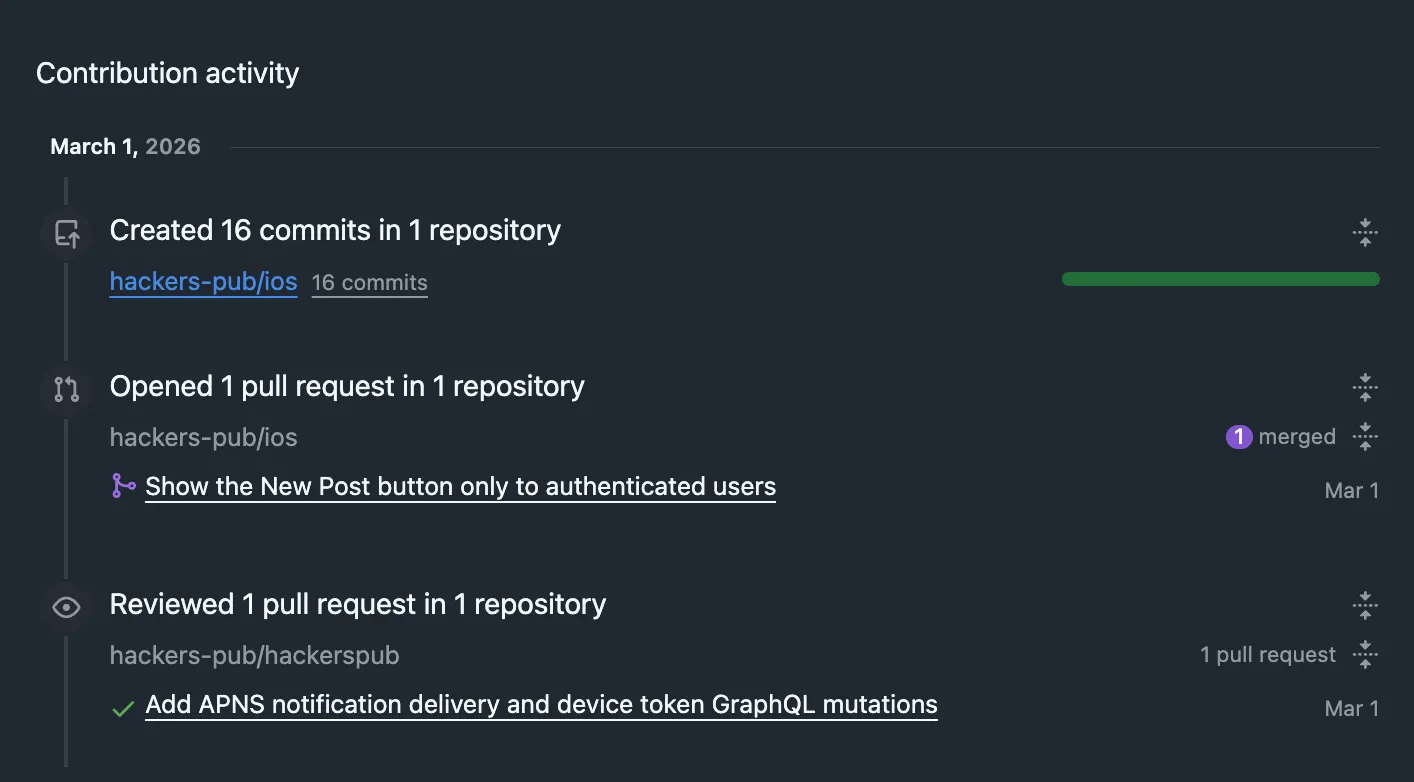
앗! 나도 해커스펍 기여자? Hackers Pub 기여자 모임 스프린트
Hackers' Pub 리뉴얼, 손꼽아 기다리고 계시지 않으신가요? Hackers' Pub, 한 번쯤 직접 기여해 보고 싶다는 생각, 해보신 적 없으신가요? Hackers' Pub, 이용하면서 어딘가 아쉽다 느꼈던 부분, 혹시 있지 않으셨나요? 이번 스프린트 모임은 리뉴얼 진도도 팍팍 빼면서, 기여자들끼리 서로 얼굴도 익히고 친분도 쌓는 자리입니다. 부담 없이 참여해 주세요. 모임은 서울특별시 성동구 상원길 26, 뚝섬역 5번 출구 근처 어딘가에 있는 튜링의 사과에서 진행합니다. 일정은 3월 1일 ~ 3월 2일. 모여서 각자 편하게 해커스펍 기여하다가 가시면 됩니다. 몸만 오시면 됩니다. 비용은 튜링의 사과 이용료만 챙겨 주시면 돼요. 감사합니다. 이 글은 연합우주를 위한 모임 개최 서비스 moim.live의 첫 게시글로 영광스럽게 공유합니다
📅 2026-03-01T02:00:00.000Z — 2026-03-02T10:00:00.000Z
Organized by: @hongminhee@hollo.social
앗! 나도 해커스펍 기여자? Hackers Pub 기여자 모임 스프린트 — Hackers' Pub (@hackerspub@moim.live)
Hackers' Pub 리뉴얼, 손꼽아 기다리고 계시지 않으신가요? Hackers' Pub, 한 번쯤 직접 기여해 보고 싶다는 생각, 해보신 적 없으신가요? Hackers' Pub, 이용하면서 어딘가 아쉽다 느꼈던 부분, 혹시 있지 않으셨나요? 이번 스프린트 모임은 리뉴얼 진도도 팍팍 빼면서, 기여자들끼리 서로 얼굴도 익히고 친분도 쌓는 자리입니다. 부담 없이 참여해 주세요. 모임은 서울특별시 성동구 상원길 26, 뚝섬역 5번 출구 근처 어딘가에 있는 튜링의 사과에서 진행합니다. 일정은 3월 1일 ~ 3월 2일. 모여서 각자 편하게 해커스펍 기여하다가 가시면 됩니다. 몸만 오시면 됩니다. 비용은 튜링의 사과 이용료만 챙겨 주시면 돼요. 감사합니다. 이 글은 연합우주를 위한 모임 개최 서비스 moim.live의 첫 게시글로 영광스럽게 공유합니다
moim.live
Link author: ![]() Hackers' Pub@hackerspub@moim.live
Hackers' Pub@hackerspub@moim.live
Starting with Deno 2.7, you can now use the Temporal API without the --unstable-temporal flag!
회사에 프론트엔드 포지션이 예상치 못하게 공석이 되어 진정한 풀스택으로 거듭나게 되었다. 다행히 중요한 것들은 구현이 마무리되서 코드 정리만 좀 하면 될 듯
나는 한 사람이 AI로 일주일만에 만들었다는게 소구점이 되는지 잘 모르겠다 https://blog.cloudflare.com/vinext/
지난주 Astro를 인수한 클플이 Next.js를 조롱하기 위해 만들었다는 의견이 그럴듯해보임
나는 한 사람이 AI로 일주일만에 만들었다는게 소구점이 되는지 잘 모르겠다 https://blog.cloudflare.com/vinext/
One thing I find a bit disappointing is that the Sanitizer API is [Exposed=Window] only, so there's no way to use it server-side in Node.js or Deno. A simple sanitize(html: string): string method would have been enough to retire a whole category of npm packages. The irony is that sanitizing untrusted HTML is arguably more common on the server—that's where you receive user input, store it, and render it back.
For now, server-side JavaScript still has to rely on DOMPurify (dragging jsdom along with it) or something like sanitize-html, each shipping its own HTML parser that may subtly disagree with how browsers actually parse markup—which is exactly the problem this API was supposed to solve.
The Sanitizer API landed in Firefox 148, along with element.setHTML().
This lets you fully configure how HTML strings are cleaned as they're parsed.
오늘 동료랑 모노레포 설계에 대해 이야기하다가, 아래의 내용을 근거로 모노레포 설계에 너무 많은 시간을 쓰지말고 그냥 죄다 몰빵하자고 설득했다. 내가 생각하는 올바른 워크플로우를 어차피 도입하지 못할 거고, 그 상황에서 차선책들을 늘어놓고 고민을 하느니 시간이라도 아끼자는 입장이다.
내가 가진 개발에서의 지식/경험/의견은 negative한 형태가 많은것 같다. 어떤 문제에 대한 명쾌한 해결책(positive)보다는, 어떤 문제가 어렵거나 별로 중요하지 않으니 그쪽으로 시간을 쏟지 말아야한다는 사실을 활용하게 되는 경우가 더 잦다.
A couple days ago, I got a DM from a #Bonfire user. I happily replied and sent
a follow request—but the Accept never came back, even though they hadn't
enabled manuallyApprovesFollowers. My DM reply probably never arrived either. Classic interop bug.
I checked out the Bonfire source and dug in. Turns out Bonfire hasn't implemented RFC 9421 yet, so it was silently discarding any activity signed with it. That alone would be workable, except for one more issue: Bonfire was responding 200 OK even when signature verification failed, instead of 401 Unauthorized.
This matters because Fedify implements a double-knocking mechanism—if a request signed with RFC 9421 fails, it retries with the older draft cavage signature. But since Bonfire returned 200 OK on the failed first knock, #Fedify had no reason to send a second one.
I filed two issues on the Bonfire #ActivityPub repo—one requesting RFC 9421 support, and one about returning 401 on invalid signatures. For the latter, I also sent a PR, which got merged pretty quickly: bonfire-networks/activity_pub#9.
That said, individual Bonfire instances won't pick up the fix until they actually deploy it. So in the meantime, I patched Hollo and Hackers' Pub to use draft-cavage-http-signatures-12 as the firstKnock, so Bonfire instances can at least understand the first request.
One last thing: Fedify caches whether a given server supports RFC 9421, and the Bonfire servers I'd already talked to were cached as “supports RFC 9421”—because they'd been returning 200 OK. I had to manually clear that cache on both hollo.social and hackers.pub before everything finally worked.
After all that, the mutual follow went through and my DM reply landed. Worth it.
The really cool thing about this new architecture is that it can enable Client to Server architecture for AP with fedify (maybe vocab packages could be used in the browser too!)
Fedify 2.0.0 is here!
This is the biggest release in Fedify's history. Here are the highlights:
- Modular architecture — The monolithic
@fedify/fedifypackage has been broken up into focused, independent packages:@fedify/vocab,@fedify/vocab-runtime,@fedify/vocab-tools,@fedify/webfinger, and more. Smaller bundles, cleaner imports, and the ability to extend ActivityPub with custom vocabulary types. - Real-time debug dashboard — The new
@fedify/debuggerpackage gives you a live dashboard at/__debug__/showing all your federation traffic: traces, activity details, signature verification, and correlated logs. Just wrap yourFederationobject and you're done. - ActivityPub relay support — First-class relay support via
@fedify/relayand thefedify relayCLI command. Supports both Mastodon-style and LitePub-style relay protocols (FEP-ae0c). - Ordered message delivery — The new
orderingKeyoption solves the “zombie post” problem where aDeletearrives before itsCreate. Activities sharing the same key are guaranteed to be delivered in FIFO order. - Permanent failure handling —
setOutboxPermanentFailureHandler()lets you react when a remote inbox returns 404 or 410, so you can clean up unreachable followers instead of retrying forever.
Other changes include content negotiation at the middleware level, @fedify/lint for shared linting rules, @fedify/create for quick project scaffolding, CLI config files, native Node.js/Bun CLI support, and many bug fixes.
This release includes significant contributions from Korea's OSSCA participants. Huge thanks to everyone involved!
This is a major release with breaking changes—please check the migration guide before upgrading.
Full release notes: https://github.com/fedify-dev/fedify/discussions/580
Modular architecture — The monolithic @fedify/fedify package has been broken up into focused, independent packages:woo! that's excellent news! i had a handful of (not currently maintained or used) libraries i wrote myself (codeberg.org/outpost/ts-libs) because all the alternatives either did too much (fedify before this) or weren't that great (the existing http signature library does not do typescript from what i can tell)
having these building blocks without the opinionated framework on top is a great step in enabling flexibility in system design without making everyone reinvent the wheel and get it wrong, excited to see this!
Fedify 2.0.0 is here!
This is the biggest release in Fedify's history. Here are the highlights:
- Modular architecture — The monolithic
@fedify/fedifypackage has been broken up into focused, independent packages:@fedify/vocab,@fedify/vocab-runtime,@fedify/vocab-tools,@fedify/webfinger, and more. Smaller bundles, cleaner imports, and the ability to extend ActivityPub with custom vocabulary types. - Real-time debug dashboard — The new
@fedify/debuggerpackage gives you a live dashboard at/__debug__/showing all your federation traffic: traces, activity details, signature verification, and correlated logs. Just wrap yourFederationobject and you're done. - ActivityPub relay support — First-class relay support via
@fedify/relayand thefedify relayCLI command. Supports both Mastodon-style and LitePub-style relay protocols (FEP-ae0c). - Ordered message delivery — The new
orderingKeyoption solves the “zombie post” problem where aDeletearrives before itsCreate. Activities sharing the same key are guaranteed to be delivered in FIFO order. - Permanent failure handling —
setOutboxPermanentFailureHandler()lets you react when a remote inbox returns 404 or 410, so you can clean up unreachable followers instead of retrying forever.
Other changes include content negotiation at the middleware level, @fedify/lint for shared linting rules, @fedify/create for quick project scaffolding, CLI config files, native Node.js/Bun CLI support, and many bug fixes.
This release includes significant contributions from Korea's OSSCA participants. Huge thanks to everyone involved!
This is a major release with breaking changes—please check the migration guide before upgrading.
Full release notes: https://github.com/fedify-dev/fedify/discussions/580
Fedify 2.0.0을 릴리스했습니다!
Fedify 역사상 가장 큰 릴리스입니다. 주요 변경 사항을 소개합니다:
- 모듈형 아키텍처 — 기존의 단일
@fedify/fedify패키지를@fedify/vocab,@fedify/vocab-runtime,@fedify/vocab-tools,@fedify/webfinger등 독립적인 패키지들로 분리했습니다. 번들 크기가 줄어들고, 임포트가 깔끔해지며, 커스텀 어휘 타입으로 ActivityPub을 확장할 수도 있습니다. - 실시간 디버그 대시보드 — 새로운
@fedify/debugger패키지로/__debug__/경로에 라이브 대시보드를 띄울 수 있습니다. 연합 트래픽의 트레이스, 액티비티 상세, 서명 검증, 로그까지 한눈에 확인할 수 있습니다. 기존Federation객체를 감싸기만 하면 됩니다. - ActivityPub 릴레이 지원 —
@fedify/relay패키지와fedify relayCLI 명령어로 릴레이 서버를 바로 띄울 수 있습니다. Mastodon 방식과 LitePub 방식 모두 지원합니다(FEP-ae0c). - 순서 보장 메시지 전달 — 새로운
orderingKey옵션으로 “좀비 포스트” 문제를 해결합니다.Delete가Create보다 먼저 도착하는 문제가 더 이상 발생하지 않습니다. 같은 키를 공유하는 액티비티는 FIFO 순서가 보장됩니다. - 영구 전달 실패 처리 —
setOutboxPermanentFailureHandler()로 원격 인박스가 404나 410을 반환할 때 대응할 수 있습니다. 도달 불가능한 팔로워를 정리하는 등의 처리가 가능합니다.
이 외에도 미들웨어 수준의 콘텐츠 협상, @fedify/lint, @fedify/create, CLI 설정 파일, 네이티브 Node.js/Bun CLI 지원, 다수의 버그 수정 등이 포함되어 있습니다.
이번 릴리스에는 한국 OSSCA (오픈소스 컨트리뷰션 아카데미) 참가자분들의 큰 기여가 담겨 있습니다. 참여해 주신 모든 분께 감사드립니다!
브레이킹 체인지가 포함된 메이저 릴리스입니다. 업그레이드 전에 마이그레이션 가이드를 꼭 확인해 주세요.
전체 릴리스 노트: https://github.com/fedify-dev/fedify/discussions/580
Fedify 2.0.0 is here!
This is the biggest release in Fedify's history. Here are the highlights:
- Modular architecture — The monolithic
@fedify/fedifypackage has been broken up into focused, independent packages:@fedify/vocab,@fedify/vocab-runtime,@fedify/vocab-tools,@fedify/webfinger, and more. Smaller bundles, cleaner imports, and the ability to extend ActivityPub with custom vocabulary types. - Real-time debug dashboard — The new
@fedify/debuggerpackage gives you a live dashboard at/__debug__/showing all your federation traffic: traces, activity details, signature verification, and correlated logs. Just wrap yourFederationobject and you're done. - ActivityPub relay support — First-class relay support via
@fedify/relayand thefedify relayCLI command. Supports both Mastodon-style and LitePub-style relay protocols (FEP-ae0c). - Ordered message delivery — The new
orderingKeyoption solves the “zombie post” problem where aDeletearrives before itsCreate. Activities sharing the same key are guaranteed to be delivered in FIFO order. - Permanent failure handling —
setOutboxPermanentFailureHandler()lets you react when a remote inbox returns 404 or 410, so you can clean up unreachable followers instead of retrying forever.
Other changes include content negotiation at the middleware level, @fedify/lint for shared linting rules, @fedify/create for quick project scaffolding, CLI config files, native Node.js/Bun CLI support, and many bug fixes.
This release includes significant contributions from Korea's OSSCA participants. Huge thanks to everyone involved!
This is a major release with breaking changes—please check the migration guide before upgrading.
Full release notes: https://github.com/fedify-dev/fedify/discussions/580
리트코드 3월 안에 다 푸는 게 목표...🥲
항상 감사합니다 🙇🙇🙇
오래 기다리셨습니다!!!
BlueBase: Python으로 밑바닥부터 직접 만들어보는 DBMS
https://theeluwin.github.io/BlueBase/
결국 완성은 못했지만, 일단 공개할 수 있는 부분이라도 공개합니다.
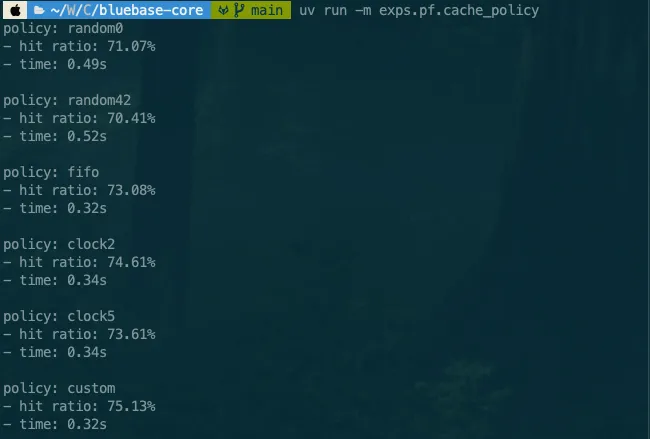
RedBase DBMS을 구성하는 PF, RM, IX, SM, QL 중 PF와 RM을 여러분들이 직접 구현 할 수 있게, 과제의 형태로 제공합니다.
PF는 paged file의 약자로, file을 page 단위로 관리하는 컴포넌트입니다. 대충 4096 바이트 단위로 관리하는데요, file에 바로바로 read하거나 write하지 않고, 자주 사용되는 page는 가능한 memory에 있도록 중간에 buffer manager를 둡니다. 그렇다면 buffer에 공간이 모자라면? buffer에 있는 page 중 누군가를 evict 할 수밖에 없습니다. 그럼 뭘 기준으로 하면 좋을까요? 이 부분을 잘 생각해서 구현해보고, 성능을 비교해보기 바랍니다. 제가 cache hit/miss 시뮬레이션 구현해둔게 있으니, 제 custom 보다 높은 성능을 달성해주세요!
이후 RM은 record management의 약자인데, PF를 사용해서 record들을 가져오거나, 새로 넣거나 등을 하게 해줍니다. 그렇다면 전체 record를 순회하는 scan 연산이 중요하겠죠. 이 부분을 구현하는 것이 핵심입니다. record는 page 앞 부분에 bitmap을 둬서 slot이 비어있는지 아닌지를 확인하는데, 만약 record 삭제 명령이 마지막 slot을 비우게 된다면 해당 page는 더이상 필요 없겠죠. 그렇지만 이를 바로 free로 만드는건 조금 비싼 연산이 필요합니다. free page list를 다시 계산해야하거든요. 그래서 보통 DBMS에서는 이러한 작업들을 vacuum 연산으로 해결합니다. 추가로, 지금은 고정 길이 record만 다룰 수 있습니다만, 가변 길이를 허용하려면 어떻게 해야할까요? 이 부분들은 자유롭게 구현해보시면 좋겠습니다.
문서와 테스트는 모두 공개되어있습니다. 기여해주시면 감사하겠습니다! 다만, 정답 코드와 핵심 로직은 마지막까지 저 혼자 해보고 싶습니다 (도전).
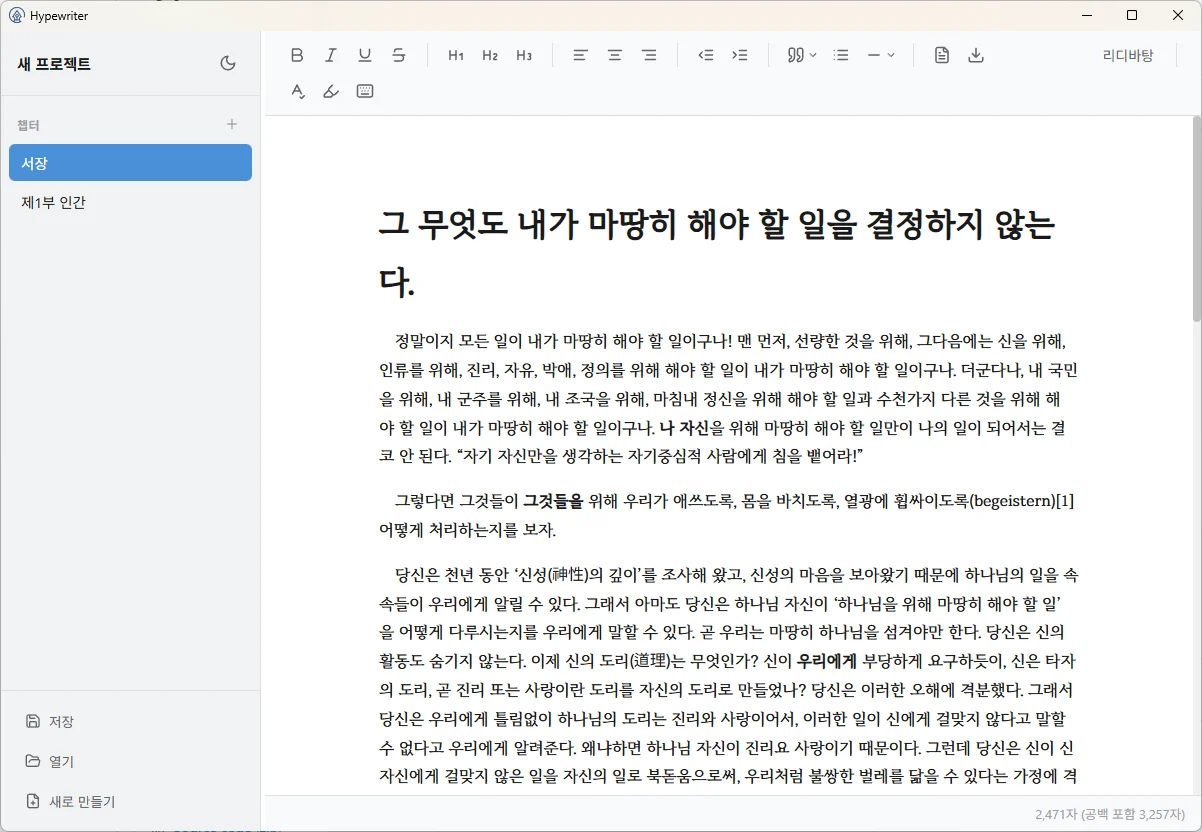
https://github.com/anxrch/hypewriter/releases/tag/v0.1.0
자신감을 갖고... Hypewriter 0.1.0을 릴리즈했습니다.
취미로 글을 쓰시는 분들(속칭 글러)을 위한 프로그램 개발을 목표로 하고 있습니다.
현재 pdf, docx, txt로 내보내기를 지원하며([그림 2] 참조)
그 외에도 글자수세기, 타자기 모드, 마크다운 문법 일부 지원, 다양한 구분선 및 인용 스타일 등을 지원합니다.
아직까진 부족함이 많지만... 잘 부탁드립니다.