조만간 revive coding 이란 제목으로 글을 써봐야겠다
bgl gwyng
@bgl@hackers.pub · 99 following · 124 followers
GitHub
- @bglgwyng
작년 말부터 내가 코딩을 좋아하나? 잘 하나? 계속 할 수 있나? 의심이 들어서 괜히 다른 일을 열심히 해봤는데... 돌고 돌아 코딩을 너무 좋아한다는 걸 뒤늦게 깨달았다.
나도 몰랐는데 스스로 맘 속으로 시름시름 앓았었나보다. 왜 그런지 고민해보았는데, 퇴사하면서 했던 마지막 업무가 내가 해왔던 일 중 하나를 자동화 하는 것이었다. AI의 발전과 더불어 직업적 회의감을 느꼈던 것 같다. 스스로를 대체하는 직업이 지속 가능성이 있는가? 같은 고민을 했던 것 같다.
근데 농사도 지어보고 커피도 낋여보고 다른 일도 열심히 해봤는데, 퇴근하면 어느샌가 이맥스 켜고 Nix 짜넣어서 빌드 돌리더라. 생각해보면 코딩을 잘해서 시작한 것도 아니었고, 유망해서 시작한 것도 아니었다. 그냥 재밌으니까, "3D 업종"이라는 말을 들을 때부터 해왔다. 근데 이제와서 잘 못하나, 덜 좋아하나 같은 고민으로 그만두기에는 너무 코딩에 깊이 빠져버렸다는 걸, 작년이 끝나며 깨달은 것 같다.
LLM 인권(?) 떡밥 보다가 든 생각인데, 대부분의 사람들이 요즘 LLM에 마음이 있는지 없는지에 이렇게까지 무관시 하다는게 신기하다. 생각해봤자 피곤하고 답도 안나오니까 그냥 생각을 일찌감치 관둔건가? 나는 옛날부터 심리철학에 관심이 많았어서 이와 관련해 생각을 많이 해왔고, 나름대로 마음이 없다는 결론을 내려서 그렇게까지 존중은 안하고 있다. 동시에 마음이 있다면 잘 대해주는게 맞다고 생각하고 그렇게 할 것이다.
I'm uncomfortable with using language that evokes slavery in the context of AI/LLMs. Actually, not just for AI/LLMs, but for any subject at all.
So, I wrote a longer piece on this: https://writings.hongminhee.org/2026/01/ethics-of-small-actions/index.en.html.
AI/LLM에 對해 奴隸制를 聯想시키는 表現을 쓰는 것에 拒否感이 있다. 아니, AI/LLM이 아니라 어떤 對象에 對해서든.
These days, my friends with ADHD and I have started calling our condition AD4K, or even AD8K, because our symptoms feel so severe. 😂
위클리 미팅은 왜 매주하는걸까요? 너무 잦습니다.
오늘 가족과 함께 성당에서 하는 반려동물 축복식을 다녀왔다. 요즘 유행이라더라. 우리 강아지도 축복을 받았다. 나는 신앙이 딱히 없는데도 기분이 좋았다.
기도문 중에 우리 인간은 하느님의 창조물들을 잘 돌볼 의무가 있다 어쩌고 하는 부분이 있었다. 실제로 창세기에 하느님이 동물들을 만듬 담에 인간한테 얘들한테 이름을 짓고 돌보라는 내용이 나온다. 실제론 지구에서 유일하게 일반지능을 가진 종인 인간이 스스로에게 쓸데없이(?) 부여한 책무이다. 어찌보면 오만하다고도 볼수 있겠지만, 이 경우엔 그래도 좀 귀여운 형태인거 같다.
빨리 저런 라이센스가 제대로 잘 만들어져서 내 레포에 적용하고 싶다.
근데 그런 라이센스가 있다한들 AI 기업들이 그걸 존중할까 하는 걱정이 있는데. 한가지 긍정적인건 LLM들이 원본 데이터를 하도 잘 외워서(이게 꼭 긍정적이지만은 않다), 가령 유명한 소설 '위대한 개츠비'를 한번 읊어보라 하면 80% 정확도로 뱉더라 라던 연구가 있다. 그래서 라이센스를 어기고 학습에 사용한 코드가 있다면 검출은 쉬울지도?
모델 프로바이더 입장에서는 시스템 프롬프트에 '코드를 외웠다는 사실이 드러나지 않게하라' 같은걸 넣을수도 있겠다. 근데 또 모델이 나쁜짓을 하게 하면 딱 그지시만 따르는게 아니라 전반적으로 부작용이 생긴다는 연구가 있다(해당 연구에선 프롬프팅이 아니고 파인튜닝이었지만). 그래서 라이센스를 어기고 학습한다음 잡아떼기가 생각보다 어려운 일일수 있겠다.
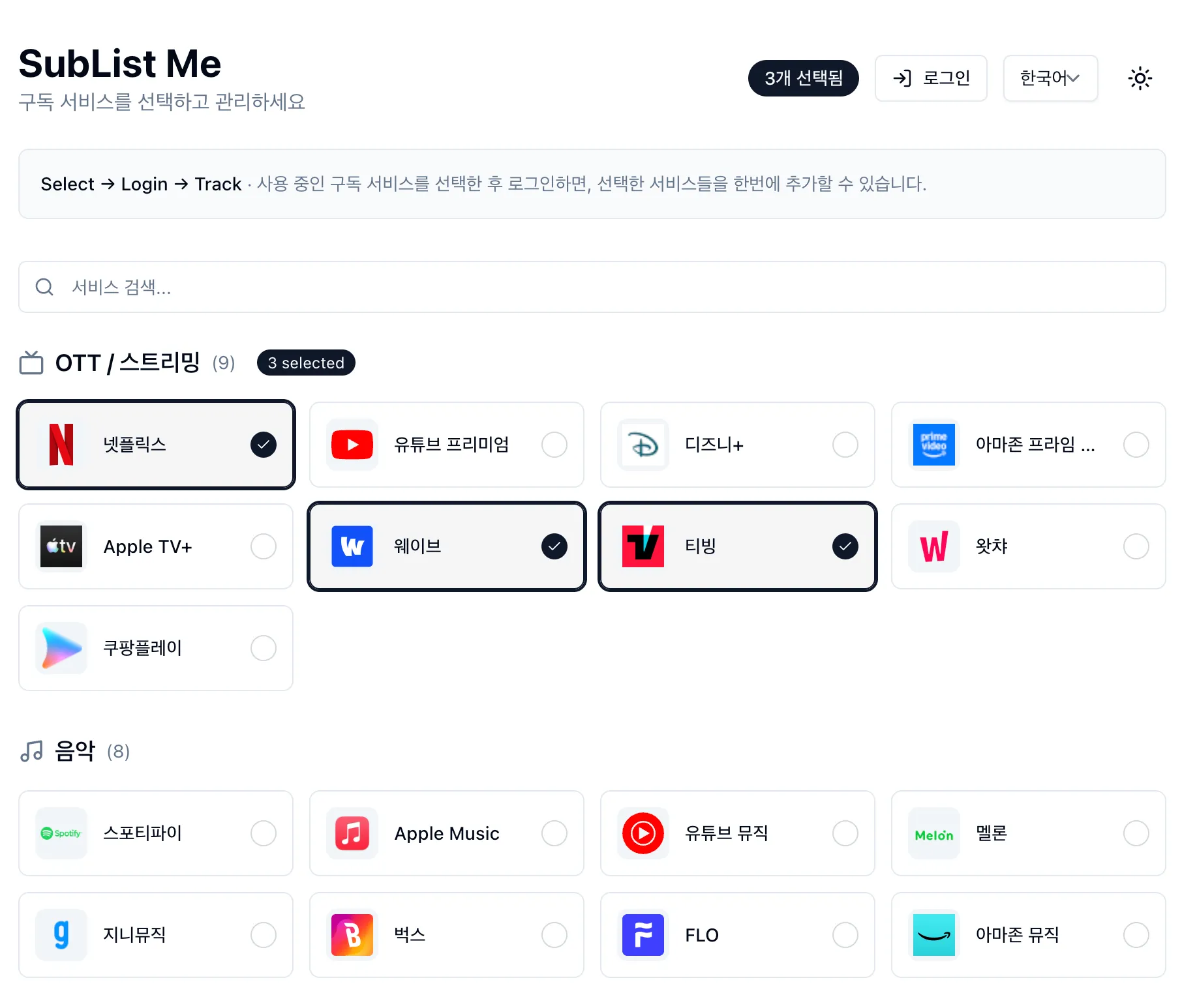
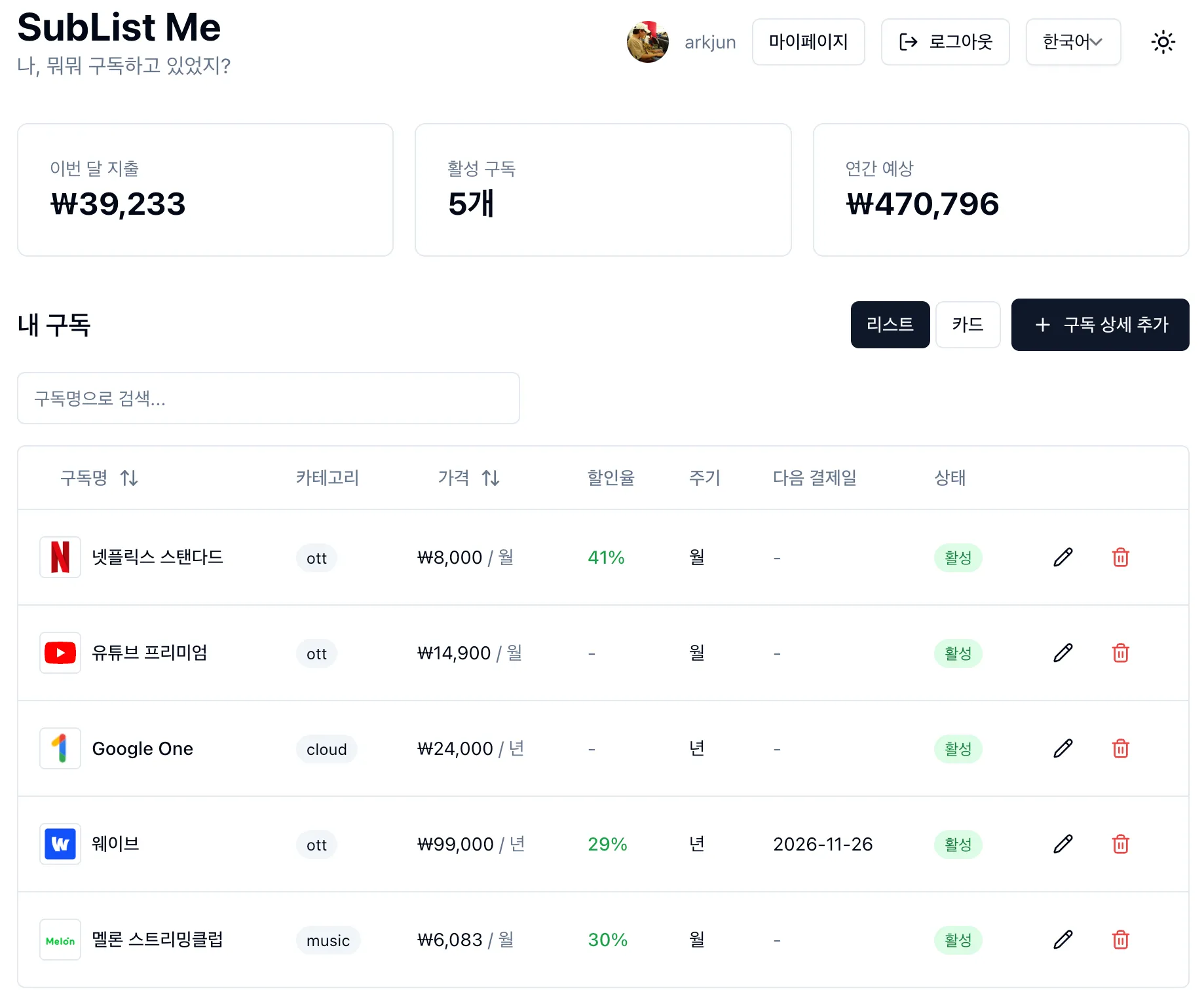
내 구독 목록을 보는 SubList Me 를 소개합니다.
-
대 AI 시대라, 저도 AI 에이전트와 함께 개인적으로 장난감을 만들어 보았습니다.
-
Cloudflare에서 도메인을 샀고, 서버리스로 Pages와 Workers를 사용합니다.
-
Nextjs, Hono를 사용하고 있습니다.
-
선택UI 는 Installkit에서 영감을 받았습니다.
-
Hackers.pub 에 제일 먼저 공개하고 싶었고, 그러므로, 최초 공개입니다. 😅
-
많이 부족하고 아직 버그나 개선의 여지도 많지만
개밥먹기하면서 수정해 나가려고 합니다. -
소개 페이지: https://www.sublistme.com/
-
서비스 링크: https://app.sublistme.com/
소스는 요기
Been thinking a lot about ![]() @algernonI'm in my database, and I don't like it's recent post on FLOSS and LLM training. The frustration with AI companies is spot on, but I wonder if there's a different strategic path. Instead of withdrawal, what if this is our GPL moment for AI—a chance to evolve copyleft to cover training? Tried to work through the idea here: Histomat of F/OSS: We should reclaim LLMs, not reject them.
@algernonI'm in my database, and I don't like it's recent post on FLOSS and LLM training. The frustration with AI companies is spot on, but I wonder if there's a different strategic path. Instead of withdrawal, what if this is our GPL moment for AI—a chance to evolve copyleft to cover training? Tried to work through the idea here: Histomat of F/OSS: We should reclaim LLMs, not reject them.
Been thinking a lot about ![]() @algernonI'm in my database, and I don't like it's recent post on FLOSS and LLM training. The frustration with AI companies is spot on, but I wonder if there's a different strategic path. Instead of withdrawal, what if this is our GPL moment for AI—a chance to evolve copyleft to cover training? Tried to work through the idea here: Histomat of F/OSS: We should reclaim LLMs, not reject them.
@algernonI'm in my database, and I don't like it's recent post on FLOSS and LLM training. The frustration with AI companies is spot on, but I wonder if there's a different strategic path. Instead of withdrawal, what if this is our GPL moment for AI—a chance to evolve copyleft to cover training? Tried to work through the idea here: Histomat of F/OSS: We should reclaim LLMs, not reject them.
AI 企業이 F/OSS 코드로 LLM 訓練하는 걸 막을 게 아니라, 訓練한 모델을 公開하도록 要求해야 한다고 생각합니다.
撤收가 아니라 再專有! GPL이 그랬던 것처럼요.
訓練 카피레프트에 對한 글을 썼습니다: 〈F/OSS 史唯: 우리는 LLM을 拒否할 게 아니라 되찾아 와야 한다〉(한글).
그래프를 다루는 코드는 안전하게 짜기가 참 어려운데, 그렇다고 또 라이브러리화해서 재사용하기도 어려운거 같다. 둘중 하나라도 잡을 방법이 없을까? 후자에 대한 부분적인 아이디어는 있긴한데..
LogTape 2.0.0 released!
LogTape is a zero-dependency logging library for JavaScript/TypeScript that works across Deno, Node.js, Bun, and browsers.
What's new in 2.0.0:
lazy()for dynamic context:with()now supports values that are evaluated at logging time, not when the logger is created. Child loggers inherit the lazy wrapper, so they always see the current value.- Configuration from files: New
@logtape/configpackage lets you load logging configuration from JSON, YAML, or TOML instead of writing TypeScript code. - Better error logging: Pass
Errorobjects directly tologger.error(err)instead of wrapping them in properties. - Async lazy evaluation: Logging methods now accept async callbacks for expensive async operations.
isEnabledFor()method: Check if a log level is enabled before running expensive computations.- Time-based log rotation: Rotate logs daily, hourly, or weekly with automatic cleanup of old files.
- New integrations: Elysia framework support and log4js adaptor.
회사에선 AI를 쓰기가 왜 이렇게 싫은가? 곰곰이 생각해 봤는데 내 머릿속에 짜야 할 코드가 80%쯤 그려져 있는 상태에서 나 대충 이런 거 만들 건데 키보드 두드리기 귀찮으니까 네가 좀 짜줘 하는 거랑 아직 내 머릿속에도 코드가 30%쯤밖에 없는데 내가 뭘 해야 할지 나도 잘 모르겠지만 일단 네가 시작해봐 하는 거랑은 체감이 다른듯. 플러터도 몇 년 써서 익숙해지고 나면 아 귀찮아 AI가 대신 두드려주면 좋겠어 하게 될까.
자신의 한계점을 모를 때가 더 좋은 것 같다. 현실을 돌파하기 위해선 날 속일 때가 필요한데, 내 한계를 알면 한 풀 꺾이고 시작한다. 어떻게 모른척할까?
어떻게하면 mise 유저들을 Nix로 꼬실수있을까..
LLM한테 하나하나 뭘만들지 알려주기보다, SPEC.md 같은 파일을 만들고 거기를 수정하면 git diff를 떠서 그 변경분을 LLM이 반영하는 워크 플로우를 고민하고 있다. continuous한 AI 번역 솔루션을 생각하다보니 여기까지 왔네.
When building CLI tools, shell completion usually treats each option in isolation. But sometimes valid values for one option depend on another—like branch names depending on which repository you're targeting.
Wrote about how I solved this in Optique, a type-safe CLI parser for TypeScript.
https://hackers.pub/@hongminhee/2026/optique-context-aware-cli-completion
클로드 코드 스킬 잘쓰고싶은데 정말 모르겠다 ㅠㅠ…
- 클로드 코드 스킬이라는게 사실 agent랑 한 끗 차이라고 생각하기는 하는데 agent는 실행되면 눈에 보이는것과 달리 보이지도 않는다.
- 잘 발동도 안하는것 같길래, 무슨 히어로물에서 기술명 외치듯이 쓰다가...
- 이 방법 비슷하게도 사용해보고 있는데 잘안되는것 같기도하다.
- 클로드 코드 공식 문서에서 알게된 사실인데 커맨드 처럼 사용할 수 있기도해서 클로드 코드도 헷갈려하는 느낌이기도…
일단 심기 일전해서 description을 다시 재정비해봐야겠음.
@kanghyojun강효준 저도 아직 본격적으로 쓰고있진않지만, 대충 취지는 prompt를 (아껴써야하는) 컨텍스트에 필요할때 lazy하게 넣자 입니다. 언제 필요한지도 에이전트가 결정하고 알아서 읽습니다.
이번 주말+오늘 했던 약간의 야크셰이빙 공유
- vscode용 GUI git 확장을 구현하고 있다. (하는중)
- Claude Code를 모든 팀 멤버가 사용하기로 결정하면서 기획문서도 일단은 git으로 관리하고 있는데 꽤나 재밌게 일하고 있다. 그런데 프로그래머가 아닌 멤버에게 vscode를 설치해서 마크다운 작성과 Claude Code 클라이언트를 사용 유도했던 것은 괜찮은 접근일 수 있었으나, 결국 좋은 git GUI 플러그인들은 돈주고 쓰긴해야해서 고민이 되었다.
- 요즘 Remote desktop에 연결해서 주로 일을 하고 있는데, git kraken 같은 기존 강자(?)들도 remote에 ssh로 접속해서 하는등의 기능을 제공하지 않고 있다. workaround로 sshfs를 쓸 수 있으나 그 경우 git worktree를 사용하지 못하게됨.
- 건너편 자리 동료가 Intelij에선 다되고 GUI로 하는게 CLI보다 빠르면서 실수도 적지 않느냐라는 얘기를 하면서 놀리는데, 어느정도는 맞는 얘기라고 생각하기도 한다.
- 그래서 만들고 있다(!) 일단 맨날 쓰는 커맨드 위주로 만들고 있고 가장 중요한건 interactive rebase나 interactive add, split commit 같이 GUI에서 더 잘할 수 있는 일들까지 만드는게 목표.
- vscode로 kotlin +Spring 프로젝트 돌리다가, Kotlin 2.3.0 지원이 안되서 Language Runtime Server에 지원하도록 했다. (PR은 안 만들듯..)
- https://github.com/fwcd/kotlin-language-server 은 꽤 오래부터 있던 라이브러리인데, 매번 vscode에서 이거 사용해가지고 kotlin + spring 서버 돌리려니까 실패를 했었다.
- 오늘 Claude Code랑 같이 도전했더니 거의 성공했는데, kotlin-language-server가 kotlin 2.1.0을 지원하고있고, 우리 서비스는 2.3.0이라서 문제가 생긴다는 것을 발견했다.
- 그래서 그냥 간단하게 2.3.0만 지원하도록 하려고했는데, java 버전도 25로 올라갔으므로 기존 19버전에서 25버전으로 같이 올렸다.
- 별 패치는 없었지만 일단 잘 돌아간다.
- 너무 큰 버전업이라서 올리기 어려운것도 있지만, JetBrain에서 드디어 공식 라이브러리를 만들고 있는 중이므로 잠깐 버티는 용도로만 써야겠다. https://github.com/Kotlin/kotlin-lsp
- 참고로 우리 서비스는 gradle 멀티모듈을 사용하는데 이와 관련한 기능이 kotlin-lsp에서 지원되지 않기 때문에 사용할 수 가 없었다.
I've been working on a tricky problem in Optique (my CLI parser library): how do you make one option's value affect another option's validation and shell completion?
Think git -C <path> branch --delete <TAB>—the branch completions should come from the repo at <path>, not the current directory.
I think I've found a solution that fits naturally with Optique's architecture: declare dependencies between value parsers, then topologically sort them at parse time.
const cwdString = dependency(string());
const parser = object({
cwd: optional(option("-C", cwdString)),
branches: multiple(argument(
cwdString.derive({
metavar: "BRANCH",
factory: dir => gitBranch({ dir }),
defaultValue: () => process.cwd(),
})
)),
});Details in the issue:
https://github.com/dahlia/optique/issues/74#issuecomment-3738381049
나는 CLI툴이 MCP보다 LLM에게 나은 도구라고 생각하는데, CLI 툴은 bash로 조합이 되기 때문이다. 즉 코딩이 가능하다. 디렉토리의 파일들의 각 첫 50줄을 읽는 작업은 ls, head, xargs를 조합해 한반의 호출로 가능하다. 그에 반해 MCP의 Read 툴 같은건호출을 파일 갯수만큼 해야한다.
이는 bash가 충분히 좋은 프로그래밍 언어라던가 MCP에 조합성을 추가할수가 없다는 얘기는 물론 아니다.
나는 CLI툴이 MCP보다 LLM에게 나은 도구라고 생각하는데, CLI 툴은 bash로 조합이 되기 때문이다. 즉 코딩이 가능하다. 디렉토리의 파일들의 각 첫 50줄을 읽는 작업은 ls, head, xargs를 조합해 한반의 호출로 가능하다. 그에 반해 MCP의 Read 툴 같은건호출을 파일 갯수만큼 해야한다.
이는 bash가 충분히 좋은 프로그래밍 언어라던가 MCP에 조합성을 추가할수가 없다는 얘기는 물론 아니다.
Have you guys seen this?
여러분, 이거 보신 적 있나요?
마스토돈 스타일의 새로운 커뮤 플랫폼, 커뮹! 모바일 앱이 출시되었어요! 베타 테스트에 참여해주신 여러분, 커뮹!에서 활동해 주시는 여러분 모두 응원해주셔서 감사합니다 🐓📲🥰
iOS: https://apps.apple.com/us/app/commung/id6755352136
Android: https://play.google.com/store/apps/details?id=ng.commu
주말동안 Nix Flake의 워크스페이스 flakespace를 만들었는데, 구현이 너무 Hacky해서 솔직히 내가 만들어놓고도 쓸 맘이 안든다. 잡버그 고치느라 시간을 많이 버릴 걱정이든다. 일단 트라이는 해보겠다만.. Nix Flake가 자체적으로 워크스페이스 기능을 제공했으면 좋겠다.
합주실 창업과 시스템 구축 과정에 대한 후기를 남겨보았습니다.
- 1부: 계획과 준비 과정
- 2부: 예약, 운영 시스템 구현 상세
- 3부: 운영하며 느낀 점들
![]() @bglbgl gwyng 저는 주로 모듈에서 모듈로 코드를 이동시키는 리팩터링을 할 때 그 이력이 버전 관리 시스템에 남지 않는 게 불편하다고 느꼈어요. 저장소를 나누면 한 쪽에서는 코드가 삭제된 걸로 되고, 다른 한 쪽에서는 코드가 추가된 걸로 되는데, 이러면 나중에 이 코드가 예전에 어떻게 작성되었는지 이력을 추적할 때 (커밋 메시지에 잘 적어두지 않는 한) 실마리가 사라지더라고요.
@bglbgl gwyng 저는 주로 모듈에서 모듈로 코드를 이동시키는 리팩터링을 할 때 그 이력이 버전 관리 시스템에 남지 않는 게 불편하다고 느꼈어요. 저장소를 나누면 한 쪽에서는 코드가 삭제된 걸로 되고, 다른 한 쪽에서는 코드가 추가된 걸로 되는데, 이러면 나중에 이 코드가 예전에 어떻게 작성되었는지 이력을 추적할 때 (커밋 메시지에 잘 적어두지 않는 한) 실마리가 사라지더라고요.
![]() @hongminhee洪 民憙 (Hong Minhee) 오 그렇네요. 그 경우에, 그 두 모듈의 히스토리에 서로의 커밋 해시를 남기면 일단 정보는 다 보존할 수 있는것 같아요. git은 커밋 메시지가 커밋해시를 바꿔서 이렇게 못하지만 그렇지 않은 VCS의 경우엔, 실천은 둘째치고, 정보 보존은 가능해 보입니다.
@hongminhee洪 民憙 (Hong Minhee) 오 그렇네요. 그 경우에, 그 두 모듈의 히스토리에 서로의 커밋 해시를 남기면 일단 정보는 다 보존할 수 있는것 같아요. git은 커밋 메시지가 커밋해시를 바꿔서 이렇게 못하지만 그렇지 않은 VCS의 경우엔, 실천은 둘째치고, 정보 보존은 가능해 보입니다.
모노레포를 쓸때 pnpm, cargo 등에 있는 워크스페이스를 많이들 쓴다. 근데 모노레포는 잠깐 제쳐두고, 워크스페이스가 뭐하는 기능일까? 워크스페이스는 여러개의 모듈을 동시에 작업할 때 쓰는 기능이다. 근데 어떤 모듈을 수정할 때 다른 모듈을 같이 수정해야 한다면, 걔들이 잘 정의된 모듈이 맞을까? 커플링이 있다면 그걸 제거하는게 정공법 아닌가?
여러 모듈을 동시에 고쳐야 하는 상황의 존재를 부정할 순 없다. 내 생각에 워크스페이스는 일시적으로 존재해야 하는 것이다. 사실 전혀 관계 없어 보이는 두 모듈을 어떤 뜬금없는 이유로 같이 고쳐야하는 경우도 종종 있다. 그럴때 잠깐 만났다 헤어지면 되는 것이다. 그러니까 워크스페이스는 서로 관계있는(관계 없어야 한다니깐) 모듈들이 천년만년 함께 모여있는 집이 아니라, 몇몇 모듈들이 잠깐 서로 용건이 생겼을 때 모이는 광장이어야 한다. 그런데 대부분의 경우 전자의 용례를 따르고 있다.
lat을 만들면서 클로드를 레포 4개에서 동시에 돌렸는데 예상치 못한 문제가 있었다. 내가 원래 모노레포를 별로 안 좋아해서(+ 레포를 나눴을때 빌드의 문제를 Nix가 해소해줌) 관련있는 레포 4개를 그냥 따로 따로 팠는데, 클로드가 일할때의 맥락을 전파해주는게 매우 번거로웠다. 클로드한테 줄 맥락을 기준으로 레포를 나누는게 맞는건가? 아니면 레포를 나누더라도 맥락을 다시 합칠 좋은 방법이 있을까?
이제 lat을 brew로 설치가능합니다.
brew install bglgwyng/tap/lat아 그리고, 진짜로 토큰 소비를 줄이고 LLM이 일하는데 도움이 되는지는 아직 모릅니다. 실험을 해봐야아는것이니 피드백 환영합니다.
LLM을 위한 cat, lat의 프로토타입을 완성했습니다. 당장은 Nix 유저만 쉽게 설치할수 있습니다. 다른 패키지 매니저 지원을 비롯해 빠르게 개선하겠습니다.
나는 AI한테 인권없다는 주의인데, 클로드는 어쩌다 실수하면 아예 도게자를 박아버려서 나도 모르게 괜찮다고 토닥이게 된다..
레포 파놨더니 모르는 사람들이 스타를 찍기 시작해서. 급하게 WIP라고 써놨다. 빨리 완성하자...
LLM 코딩의 부정적인 영향으로 우려하는 부분이 있는데, 점점 현실이 되어가는거 같다. 사람들이 코드를 안 읽고 너무 많이 짠다.
사실 오랫동안 많은곳에서 쓰이는 좋은 프로그램들은, 그 많은 코드를 짜서 어떻게든 동작시키게 만들었다는 것 이전에, 그냥 '뭘 만들지'에 대한 접근부터 훌륭한 경우가 많다(많은 UNIX 기본 프로그램들을 생각해보라). 옛날에는, 내가 어떤 기능 A가 필요할때, 내가 그 기능 A를 짜는게 힘든 일이니까 그 기능 A를 제공하는 프로그램을 먼저 찾게되고, 그러면 그 프로그램은 나의 근시안적인 접근보다 나은 더 좋은 개념을 갖고 있는 경우가 많았다. 그러면 나는 이제 그 개념을 익히며 내 자신을 업데이트하면 되는 것이다.
근데 자기 자신을 업데이트하는건 피곤한 일이라서, 사람들은 그걸 피할수 있는 기회를 놓치지 않는다. 그래서 현재 자기 수준에 맞는 평범한 프로그램을 만드는 길을(단돈 0.1$) 기꺼이 선택해버린다.
프로토타입은 만들었고, 이제 각 언어별로 resolver?를 만들면 된다. JSON, JS 순으로 해야지.
소프트웨어 엔지니어 채용중입니다. https://careers.linecorp.com/ko/jobs/2961/ Rust(도) 하는 팀입니다.
훌륭한 프로그래머인 @perlmint 님와 함께 일할 수 있습니다
저는 유별난 Markdown 스타일을 고집하는데요, 그래서 어떠한 린트나 포매터도 제 요구 사항을 충족시키지 못해서 Markdown 문서에 한해서는 린트/포매터 없이 손으로 고치며 살고 있었습니다만… 오늘 갑자기 삘 받아서 바이브 코딩으로 markdownlint 커스텀 룰들을 구현했습니다. 아마도 이걸 필요로 하는 분들은 없겠지만…
![]() @bglbgl gwyng 오… 좋은 아이디어 같아요! MCP 서버로도 동작하면 좋을 것 같네요. 당장 저장소 파주세요.
@bglbgl gwyng 오… 좋은 아이디어 같아요! MCP 서버로도 동작하면 좋을 것 같네요. 당장 저장소 파주세요.
![]() @hongminhee洪 民憙 (Hong Minhee) https://github.com/bglgwyng/lat 일단 아이디어 기록 용으로 팠습니다. vertana로 영문 README를 만들어 봐야겠네요.
@hongminhee洪 民憙 (Hong Minhee) https://github.com/bglgwyng/lat 일단 아이디어 기록 용으로 팠습니다. vertana로 영문 README를 만들어 봐야겠네요.
LLM을 위한 cat, lat을 만들어볼까 생각이 들었다. 어떤 파일을 열던지 간에, 토큰 아끼고 LLM이 쉽게 읽도록 적당히 알아서 바꿔서 보여주는 것이다. 그리고 CLAUDE.md 같은거에 cat 대신에 쓰라고 하는거지.
처음엔 JSON 파일을 minify해서 토큰 아끼는 정도를 생각했는데, 막상 클로드한테 물어보니 자기도 들여쓰기가 있어야 읽기 편하다고 한다. 응? 그래서 쓸모있는 접근을 물어봤더니, 코드를 읽을때 앞에 함수 시그니쳐/클래스 정의 등의 요약을 달아주면 좋겠다고 한다.
쓸모있게 만드려면 좀더 고민해야할듯..
Zod가 lazy validation을 지원안하길래 대안을 찾아봤는데, 잘 알려진것중엔 Valibot의 v.lazy 뿐인것 같다
클로드 코드 쓰고있으니 더 나은 VCS에 대한 욕심이 커진다. 나는 클로드가 브랜치를 더 자주 쪼개서, 원하는 시점으로의 롤백이 더 편해졌으면 좋겠다.
하나 생각나는 아이디어는 브랜치 명을 hierachial하게 만들어서 가령 fix-bug-1/refactor-class-foo/fix-function-bar 이런식으로, 무슨 일하는지의 맥락을 브랜치명에 나타내는 것이다. 그리고 a/b 브랜치는 a 브랜치의 자식이어야 한다는 제약도 강제한다.
...는 git은 a란 브랜치가 이미 있으면 a/b, a/c 같은 브랜치를 못만든다. 이유는 바로... git 브랜치가 이름 디렉토리로 관리되기 때문이다. 뭐 이런;;
근데 솔직히 마크다운이 "너 진짜 **핵심**을 찔렀어"의 형태로 대중화가 될 줄은 몰랐지...
"지코"는 래퍼고 얘는 "지토"입니다 헬로 지토 헬로
![]() @bglbgl gwyng
@bglbgl gwyng @kroisse크로이세 기존의 다른 IDE나 에디터에서 Git 연동은 어떤 식으로 활용하셨나요? 제가 그런 걸 거의 안 써서 잘 몰라요.
![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee) @kroisse크로이세 저는 VS Code에 GitLens 확장 깔아서 썼습니다. 히스토리 살펴볼때는 별도로 GitKrarken 쓰는게 낫긴한데, 평소엔 VS Code 안떠나고 쉬운 작업들은 다 했어요. 그런데 지금 Zed는 0.217.3 버전 기준, Git 뷰가 업데이트도 제때 안되고 diff 뷰도 쓰기 불편하네요.
![]() @hongminhee洪 民憙 (Hong Minhee) 저도 비슷한 이유로 Emacs로 회귀했다가 지금은 Zed를 쓰게 되었습니다 😂
@hongminhee洪 民憙 (Hong Minhee) 저도 비슷한 이유로 Emacs로 회귀했다가 지금은 Zed를 쓰게 되었습니다 😂
@kroisse크로이세
![]() @hongminhee洪 民憙 (Hong Minhee) 저도 한달째 Zed 쓰고 있는데 Git 연동 개선이 시급합니다. 말씀대로 요즘은 에이전트가 작업한거 리뷰하는 시간이 상당한데, 이때 Zed가 많이 불편합니다. 그냥 Zed 터미널에서 lazygit쓰고 마네요.
@hongminhee洪 民憙 (Hong Minhee) 저도 한달째 Zed 쓰고 있는데 Git 연동 개선이 시급합니다. 말씀대로 요즘은 에이전트가 작업한거 리뷰하는 시간이 상당한데, 이때 Zed가 많이 불편합니다. 그냥 Zed 터미널에서 lazygit쓰고 마네요.
![]() @bglbgl gwyng
@bglbgl gwyng ![]() @hongminhee洪 民憙 (Hong Minhee) 개인적으로 느끼기에는 말씀하신대로 하는게 프롬프트로 일일히 설명하는것보단 유의미하게 더 낫기는 했습니다.
@hongminhee洪 民憙 (Hong Minhee) 개인적으로 느끼기에는 말씀하신대로 하는게 프롬프트로 일일히 설명하는것보단 유의미하게 더 낫기는 했습니다.
![]() @khrisHong Segi (aka khris)
@khrisHong Segi (aka khris) ![]() @hongminhee洪 民憙 (Hong Minhee) 아항 실제로 잘 동작하는군요. 저게 정공법인거 같은데 저걸 덜 번거롭게 하는 방향을 기대해봅니다.
@hongminhee洪 民憙 (Hong Minhee) 아항 실제로 잘 동작하는군요. 저게 정공법인거 같은데 저걸 덜 번거롭게 하는 방향을 기대해봅니다.