요새 슬슬 유행이 한풀 꺾인다길래 만들어보았다. 두쫀쿠.
lionhairdino
@lionhairdino@hackers.pub · 77 following · 86 followers
여행 기분내며, 여기 저기 낙서하는 https://yearit.com 을 운영 중입니다.
지금까지 다루어 봤던 언어는 아래와 같습니다. MSX Basic Z80 Assembly Pascal GW-Basic C Macromedia Director Visual Basic PHP Flash Actionscript C++ Javascript
그리고 지금은, 하스켈을 비즈니스에 쓰려고 몇 년간 노력하고 있습니다. 지금 상태는, 하스켈 자체를 연구하는 게 아니라, 하스켈 (혹은 함수형 언어) 이해가 어려운 이유를 연구하는 아마추어 연구가쯤 되어버렸습니다. 하스켈 주제로 블로그를 운영 중이지만, 아직은 하스켈 프로그래머라고 자신 있게 말하진 못하고 있습니다. 가끔 이해에 도움이 될만한 측면이 보이면, 가볍게 아이디어를 여러 SNS에 올려보곤 하는데, 그다지 프로그래머에게 쓸모 있는 내용이 포함되진 않는 것 같습니다.
Blog
- lionhairdino.github.io
YearIt
- yearit.com
ㅋㅋㅋ 굉장히 예상을 벗어난 포스트입니다. ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
AI가 작업하는 모습을 보고 있자니, 옛날 쉘 스크립트나 펄 계통 마스터들은 프로그래밍할 때 자동화를 많이 했겠구나 싶다. 이런 것 까지 스크립트로 해결하는구나 하고 감탄할 때가 많다.
Miles Deutscher 님의 프롬프트를 보니, 이런 거 잘하는 사람들이 유능한 프로그래머가 되는 거겠지요? 문예창작과 비스무레한 전공 파트가 생기겠는데요.
수박 겉핥기 식으로 알고 있는 pm이, 팀원에게 “요즘 이렇게들 많이 한다는데, 이렇게 하면 어때?" 칠떡같이 알아듣고 코드를 뽑아낸다.
여러 수박을 핥아야 하는 직업군이 된 것 같다.
문득 요즘은 프로그램 짠다는 말보다는 프로그래밍 한다가 더 많이 쓰이는 것 같은데요. 다른 분들은 어떤가요?
꿈보다 해몽 중이다. 일단 기능을 밀어 넣고, 이리 저리 써보며, 합리화 방법을 찾다가 없으면 비활성화 한다. 서비스가 몇 번의 피벗을 하고 있는지 모르겠다. 애초 생각대로 개발 안하는 게 정상이다라고 스스로를 달래고 있다.
뛰어난 기획자 자질로, 만들기 전에 머리 속에서 시뮬레이션이 끝나야 하는데, 내가 날 못 믿는다.
꿈보다 해몽 중이다. 일단 기능을 밀어 넣고, 이리 저리 써보며, 합리화 방법을 찾다가 없으면 비활성화 한다. 서비스가 몇 번의 피벗을 하고 있는지 모르겠다. 애초 생각대로 개발 안하는 게 정상이다라고 스스로를 달래고 있다.
![]() @lionhairdino 미리 찍어두고 나눠줍니다 ㅎㅎ 가끔 궁금해하는 분 계시면 직접 찍게 해드려요!
@lionhairdino 미리 찍어두고 나눠줍니다 ㅎㅎ 가끔 궁금해하는 분 계시면 직접 찍게 해드려요!
저는 만나 뵈면 직접 찍겠습니다.![]() @jihyeokJihyeok Seo
@jihyeokJihyeok Seo
팔로우분들이 몇 십명 뿐이 없지만, 개인 SNS 계정들에 서비스 홍보 소식을 가끔 올려 왔습니다. 그런데, 처음 올렸을 때보다 점점 좋아요나 노출 빈도가 떨어지는 것 같아, 팔로우분들이 피로감이 들어서 그런가보다 했는데, 물론, 이 이유도 없진 않겠지만, SNS 알고리즘 자체가 같은 해시 태그로 여러 번 올리면, 스팸 시그널로 받아 들일 수 있다는 것 같습니다. 이 건 몰랐네요.
서비스 홍보 글을 작성하는데, 카테고리가 애매합니다. SNS도 아니고, 그렇다고 블로그도 아니고.
낱 개의 글을 올리며 공유를 하니 SNS같지만, 팔로우 같은 건 없고, 비휘발성이고,
개인 노트를 만들어 글을 올리니 블로그 같지만, 딱 타임라인에 맞게 글이 정렬되지는 않습니다.
사람들은 쉽게 받아들이기 위해 카테고리를 우선 찾는 데 안착할 카테고리가 없네요.
Drop dots. Leave comments. On maps or images.
당장은 위 설명으로 밀고 가려하는데, 대충 감이 오는 문장인가요?
![]() @lionhairdino 오픈스트리트맵의 세계는 언제나 여러분을 기다리고 있습니다
@lionhairdino 오픈스트리트맵의 세계는 언제나 여러분을 기다리고 있습니다
구글맵의 Attribution을 보아 하니, 구글맵은 여러 나라의 지도 서비스와 제휴하는 것 같은데요. 우리나라는 SK지도를 받아다 쓰나봐요. 구글 지도도 네이버나, 카카오보다는 정보 신선함이 떨어지긴 하는데 그래도 오픈맵 보다는 요즘 정보가 많이 나오긴 합니다. 다이나믹으로 넘어가면 그래도 쓸만해 보이긴 하던데요. 요금 폭탄 터질 조짐이 보이면 방어하기 위해 오픈스트리트맵 설정을 강제하는 기능을 넣어 놓긴 했습니다. ![]() @akastoot악하
@akastoot악하
구글맵타일 API 요금이 6만원이 나왔다. 초기 공짜 기간이 끝나서 그려려니 할 수 있는 금액인데, 접속자가 거의 없는 상황에서 개발에만 쓰였는데, 비용이 더 나온 느낌이다. 프록시 캐싱, http 캐싱, 구글맵 세션 등이 정상적으로 동작하지 않고 있는 건가? 다시 확인하니, 새로고침 할 때마다 타일을 매번 불러온다. 6만원이 나갔으니, 여섯 끼 굶고 반성해야겠다. (연속으로 굶지는 않고, 6일동안 아침만 걸러야지.)
The physical name card looks like this.
이 건 줄때마다 도장 찍어서 줘야 하는 명함인가요? ![]() @jihyeokJihyeok Seo
@jihyeokJihyeok Seo
한 때 만들고 싶었던 스타일의 책입니다. 내용 말고 스타일. https://cartesian.app/
"개발자가 기술을 못 쫓아가면 점점 도태된다" 이견이 없는 문장이었는데, 달라질지도 모르겠다. 지금 나오는 수많은 LLM과 대화하는 기술들은, 짧게는 몇 달 길게는 1~2년 정도만 쓸 임시적인 장치들 같다. AI는 점점 똑똑해지고, 수많은 과도기용 스킬, 테크닉들은 사라지리라는 예측은 어렵지 않다. "이렇게 말하면 LLM이 말을 잘 들어 먹더라"는 장치들을 못 쫓아가서 불안해질 때쯤이면 다음 장치들이 나온다. 계속 개발자를 하려면 필요한 재능은 이런 일시적 장치들을 잘 쓸 수 있는 능력이 아닐 것 같다.
너무 명쾌하게 답을 주네.
돈 없으면: 시간 쓰기
시간 없으면: 돈 쓰기
둘 다 없으면: 포기 또는 피봇
5년전쯤 하스켈 학교 디코에 들어가서 이게 왠 신세계인가 했다. 혼자서 하스켈과 1~2년 씨름하다 지쳐갈 무렵 하스켈 학교 디스코드를 알게 됐다. 신나게 질문하고 많이 배웠다. 어떤 주제들은 너무 잘못된 방향으로 가면서 질문을 하다 핀잔도 듣곤 했지만, 혼자 끙끙 되던 때와 비교도 안되게 진도도 나가고, 좋은 선생님, 동급생(비슷한 진도의 사람들)들도 알게 되고, 신나게 새벽까지 디코에서 질문 날리고 공부했다. 아니 놀았다.
그 전에는 좋아하는 주제로 모인 커뮤니티에 속해 본적이 없었다. 지금은 다른 디코 서버에서 서식하고 있는데, 아마도 내가 이런 문화의 끝물을 즐긴 건가 싶다. AI가 생긴 뒤로 질문 자체가 잘 안 올라오고, 올라와도 나 정도가 답할만한 질문은 거의 올라 오지 않는다. 아마도 더 이렇게 되겠지. 그 참... 한 4~5년 재밌었는데 말이다.
그나저나 내가 느끼는 AI의 최고의 장점은, 개인 교사다. 나는 그닥 영리하진 않아서, 공부, 일하다 보면, 질문하고 싶은게 쌓이는데, 잘도 대답해 준다.
위클리 미팅은 왜 매주하는걸까요? 너무 잦습니다.
이름을 다른 걸로 지어야 하지 않을까요.ㅎ ![]() @bglbgl gwyng
@bglbgl gwyng
지금 만들고 있는 서비스의 카테고리가 결정됐다. Dot-based social platform 기존에 이런 용어 없다고? 그럼 내가 선점한다! 미쳐가는구나...
![]() @lionhairdino 이게 우울증을 불러일으키기도 하죠...
@lionhairdino 이게 우울증을 불러일으키기도 하죠...
젊었을 때 보다 심하게 치고 가네요. 기억력은 안좋아졌는데, 이런 것도 자주 까먹으면 좋겠습니다.![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
눈이 쌓여야 오랜만에 옥상에 연성진을 그리는데..
뭘 소환하시려고.![]() @akastoot악하
@akastoot악하
자신의 한계점을 모를 때가 더 좋은 것 같다. 현실을 돌파하기 위해선 날 속일 때가 필요한데, 내 한계를 알면 한 풀 꺾이고 시작한다. 어떻게 모른척할까?
https://www.youtube.com/watch?v=8VcnF40x8L0 임백준님이 영상을 올리고 있었네요. 예전에 나는 프로그래머다 팟캐스트 종료 이 후, 언제 또 하시나 했는데요.
오늘은 내일 걱정만 하고, 모레 걱정은 하지 말아야 겠다.
어제 얘기한 모레 걱정, 내일의 걱정이 해결이 안되네..
소프트웨어 엔지니어 채용중입니다. https://careers.linecorp.com/ko/jobs/2961/ Rust(도) 하는 팀입니다.
훌륭한 프로그래머인 @perlmint 님와 함께 일할 수 있습니다
오늘은 내일 걱정만 하고, 모레 걱정은 하지 말아야 겠다.
X가 프리미엄 구독을 1,000원에 낚시한다.
현재 개발 중인 이어잇 서비스 계정을 프리미엄으로 전환해 뭐가 좋은지 봐야지.
12월 1일 프리미엄 전환!
절대 몇 천조 있는 회사에 놀아나지 않고, 제 때 해지할 것이다.
아이폰 달력에 해지 알림 추가.
1월 1일, "띠링~ stripe가 x 구독료 후루룩 했음"
아......... 당했다. 애플 달력이 왜 알림을 안해줬지. 애플과 X가 손잡고 있을 줄이야...
※ 그런데, 구독 후 바로 해지 예약 해 둘 걸. 왜 안해놨지란 생각이 드네요. 직 후에는 UI가 안보였었나...어쨌든, 딱히 필요성을 못 느꼈는데 몇 천조에 9,000원을 보태줬습니다.
![]() @lionhairdino 아직 있는 걸로 알고 있어요.
@lionhairdino 아직 있는 걸로 알고 있어요.
없어졌다는 소식은 못 들은 것 같고, 길에서 본 적이 없는 것 같은데, 아직 있긴 있군요. ![]() @akastoot악하
@akastoot악하
https://n.news.naver.com/article/665/0000006486?cds=news_media_pc&type=editn 덴마크가 우체통을 없앴다는데, 가만 생각해 보니 우리나라는 아직 있는지 없는지 모르겠네요.
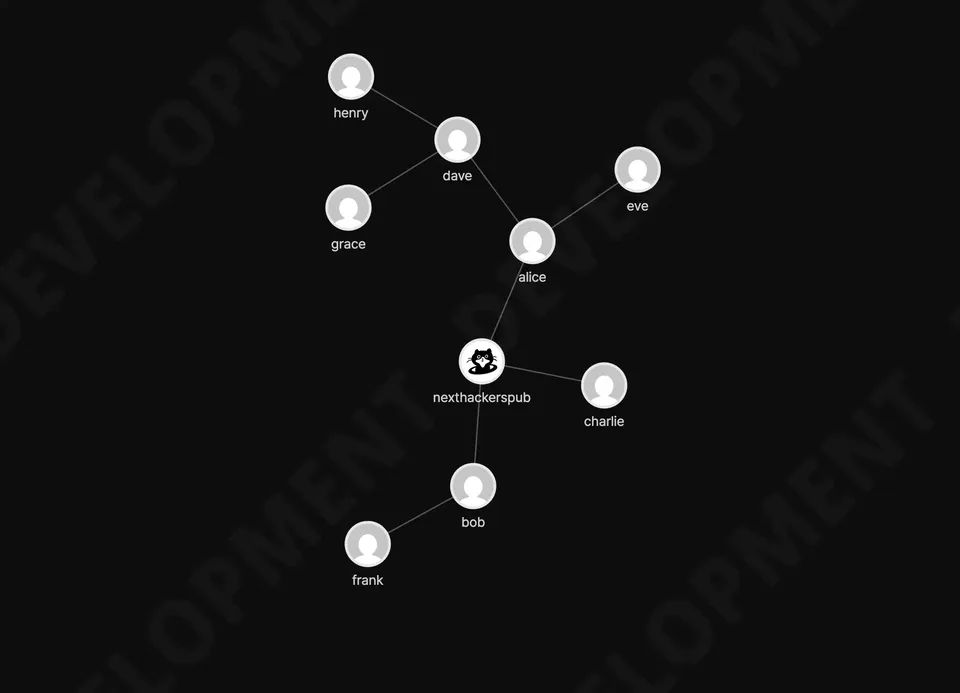
크리스마스를 맞아 크리스마스 트리... 가 아닌 Hackers' Pub 초대 트리를 꾸몄습니다.
기존 초대 트리는 작은 규모에서는 충분히 제 역할을 했으나 회원이 점차 늘어나면서 구조를 파악하기 어렵고, 페이지가 너무 길어져 변화가 필요하다고 생각했습니다. 다음 개편되는 Hackers' Pub의 초대 트리 페이지에서는 초대 관계를 잘 드러내면서, 많은 회원이 한 눈에 들어올 수 있도록 만들었습니다. Hackers' Pub의 회원은 앞으로도 많이 늘어날 예정이니까요. 그렇겠죠? 내년에도 Hackers' Pub에서 많은 분들을 만날 수 있기를, 더 풍성한 초대 트리를 볼 수 있기를 기대해봅니다.
멋지네요. 많이 있어 보입니다! 오렌지색이 잘 안보여 데이터 누락입니다...라고 하려 했더니, 저희 족보는 제 바로 위 조상님까지만 보이고 잘렸네요. ![]() @yihyunjoon이현준
@yihyunjoon이현준
![]() lionhairdino replied to the below article:
lionhairdino replied to the below article:
스마일 PRO 라식 수술 후기
자손킴 @jasonkim@hackers.pub
오랫동안 안경 생활에 익숙해져 시력 교정의 필요성을 느끼지 못하던 저자가 스쿠버 다이빙 중 겪은 불편함을 계기로 스마일PRO(SMILE Pro) 수술을 결심하고 진행한 상세한 과정을 다룹니다. 정밀 검사를 통해 각막 두께와 안압의 정상 상태를 확인하고, 노안(presbyopia) 발생 가능성을 고려하여 교정 시력을 미세하게 조정하는 상담 과정을 거쳤습니다. 수술 과정에서 레이저 조사(laser irradiation) 시 초록색 불빛에 시선을 고정하는 기술적 고충과 개인별 안구 각도에 따른 정렬 최적화의 중요성을 생생하게 묘사합니다. 수술 직후 발생하는 일시적인 눈시림과 이물감을 극복하며 시력이 점진적으로 회복되는 단계별 변화를 기록하고 있으며, 철저한 사후 관리와 안약 투여의 필요성을 강조합니다. 이 글은 시력 교정술을 고민하는 이들에게 수술 당일의 긴장감 넘치는 진행 과정과 실제 회복 단계에서 얻을 수 있는 구체적인 인사이트를 제공하며 안경 없는 새로운 삶의 가치를 전달합니다.
Read more →분명 글은 드라이한 것 같은데, 상황과 심정이 딱 그려집니다. ㅎ 탈없이 신나게 다이빙하실 바랍니다. @jasonkim자손킴
https://v.daum.net/v/20251222085555310 문득, 세상에 엄청 다양한 대상들이 존재하는데, 이론은 그들을 같은 류로 볼 수 있는 방법들을 찾는 게 목표인가 싶다.
![]() @lionhairdino 좋아해주셔서 감사합니다. 아직 재고가 남아서 다음 다음 행사에나 만들 수 있을 것 같네요..
@lionhairdino 좋아해주셔서 감사합니다. 아직 재고가 남아서 다음 다음 행사에나 만들 수 있을 것 같네요..
뭔가 밥값(키캡값)을 해야겠다는 의무감이 생겨 팔로우는 몇 안되지만, 여기 저기 SNS에 올리고 있습니다. 사진 찍으려고 모델분이 손가락에 로션도 발랐습니다. ![]() @akastoot악하
@akastoot악하
가족들이 밋업 굿즈를 탐내는 건 처음이다. 다음번엔 앵그리 버전 한 표!
tauri로 패스워드 툴 만드는 이유, 레거시 프로덕트의 지속 여부를 결정할 때 llm을 어찌 썼는지, claude skill 활용 방법, 오라클 클라우드 쓰면 왜 좋은가, 개발자가 개발을 좋아하냐, 좋아 해야만 하냐, 개발자의 ethic 등... 2025년 라스트 개발 밋업이 알차네요.
해커스펍 송년회 인기 폭발이라 참여를 못하고 튕겨져 나왔어요 ㅎㅎ. 서로 말귀!가 통하는 사람들끼리 네트워킹 시간을 가질 수 있는 귀한 기회였습니다.
뒷풀이란 말이 빠졌네요
해커스펍 송년회를 다녀왔습니다. 발표를 라이트하게 가져간다 해서 라이트하게 질문 편하게 했는데, 질문 총량이 넘어가진 않았나 걱정될 정도로 많이 한 것같아 살짝 불안하지만, 재밌었습니다.
해커스펍 송년회 인기 폭발이라 참여를 못하고 튕겨져 나왔어요 ㅎㅎ. 서로 말귀!가 통하는 사람들끼리 네트워킹 시간을 가질 수 있는 귀한 기회였습니다.
ㅠㅠㅠㅠㅠㅠㅠㅠ
커서 핸들 정도 아닐까요. 정답인지는 모르겠습니다.@eatch잇창명 EatChangmyeong💕🐱
![]() @lionhairdino https://hururuek-chapchap.tistory.com/244 맥 콘솔 앱에서 아이폰에서 발생하는 로그를 볼 수 있는 것 같습니다. 해당 현상이 발생한 시점의 로그를 확인해보면 뭔가 얻을 수 있지 않을까요?
@lionhairdino https://hururuek-chapchap.tistory.com/244 맥 콘솔 앱에서 아이폰에서 발생하는 로그를 볼 수 있는 것 같습니다. 해당 현상이 발생한 시점의 로그를 확인해보면 뭔가 얻을 수 있지 않을까요?
오, 신경 써주셔서 감사합니다. 알려주신 방법으로 살펴 볼게요. 감사합니다. @quiraxical킈락
제가 재설계한 스플릿 키보드 Mountain Breeze 공동구매를 엽니다. Choc, MX 모두 쓸 수 있고 내비게이션 클러스터가 풀배열로 탑재된 녀석입니다.
5인까지 계획중이고, 구성품은 PCB, 안티고스팅 다이오드, 3D 프린팅된 케이스, NRF Micro, 배터리입니다. Choc 쓰시는분 한정해서 스위치랑 소켓, 키캡도 같이 공구합니다.
디스코드로 모집합니다.
#키스토돈 #키보드
https://discord.gg/TdWpyCQbdE
![]() @lionhairdino 제 생각에는 OS 내지 사파리 단에서 벌어지는 일 같은데, 혹시 모바일 유튜브 웹(m.youtube.com)에서 재생해도 동일한 현상이 발생하나요?
@lionhairdino 제 생각에는 OS 내지 사파리 단에서 벌어지는 일 같은데, 혹시 모바일 유튜브 웹(m.youtube.com)에서 재생해도 동일한 현상이 발생하나요?
킈락님 말씀이 맞습니다. 아이폰 사파리에서 리셋(페이지 새로 고침)시켜 버리는 걸로 보입니다. (모바일 유튜브는 정상입니다.) 임베드 (iframe) 플레이어에서만 일어나는 것 같습니다. 대답이 전부 ~같습니다로 밖에 답을 못드릴 정도로 지금 지식이 얄팍합니다. @quiraxical킈락
"OOO 주식회사 OOO 대표님 맞으시죠? 산업안전보건교육 받아야 하는 업체에 해당합니다. 직원이나 프리랜서 고용 있으시죠? 어쩌고~" 일단 쎄한 느낌을 받았습니다. 다다다 쏴붙이면서 중간에 질문할 틈을 최대한 막으면서 가는 꼬락서니가 관공서는 아니구나 싶었습니다. 고용이나 프리랜서 없다고 하니, 뚝 끊어 버립니다. 검색해보니, 이런식의 반쯤 사기같은 행태가 존재한다고 하네요. 소규모 법인 대표님들 조심하세요~
캬... IOS 사파리에서 유튜브 플리 재생은 포기가 정답이군요. 의왼데요.
올라 올 사람들이 올라 오는 군. 라이브 보는 재미를 챙길 때가 없어, 해마다 즐겨 봅니다. 경쟁이란 설정은 취향이 아니고, 라이브가 좋아요. 오늘은 나초와 맥주 준비하고, 즐기는 중입니다.
유튜브 임베드로 4~5분짜리 영상 5개를 돌리는데, 광고가 하나도 안나온다. 뭔가 잘 못 됐다. 정책 위반했다고 막아버리면 곤란한데, 광고를 보여 달라!
아이폰 사파리 리액트 웹앱에서 모달창을 띄워 유튜브를 재생하는데 10여분이 지나면 갑자기 닫혀 버립니다.(PC는 정상) 닫히는 순간 사파리 상단에 알림창이 아주 찰나에 떴다 사라집니다. 맥북 개발자 툴에 붙여 확인했는데 별다른 로그도 안남고, 찰나에 사라진 메시지가 뭔지도 알 수가 없네요.
10분동안 재생된 영상 3~4개인데, 캐시가 얼마 되지 않아 메모리 이슈는 아니지 않을까 하는데요. 언젠가 앱개발도 손대야 할지 모르는데, 살짝 겁납니다. 디버깅 방법이 뭐가 좋을까요?
LiftIO 2025에서 받은 led 키캡 키링의 용도를 찾았습니다. 혹시 피젯스피너라고 아시나요? 정서적인 이슈가 있을 때 이용하는, 손에 쥐고 팽그르르 돌리는 장난감 같은 건데, 기계식 키(아마도 청축)가 그 역할을 하는 것 같습니다.ㅎ
지금 만들고 있는 서비스가, 어찌 보면 새로운 형태의 서비스(뭐... 그다지 새롭지 않다. 특별한 아이디어가 들어간 것도 별로 없다)가 오만하게 join 먼저 유도하고 있는 것 같아, 일단 접속하면 서비스가 보이도록 바꿨다. 일단 URL로 접속하는 사람들은 무슨 서비스인지 다 알고 온다는 가정으로 로그인 페이지를 띄웠는데, 사람들의 생각은 다른 것 같다. 뭔지 보고 쓸지 말지 결정해야지, 옆 사람 말만 듣고 결정하기엔 이미 SNS는 넘쳐난다. 혼자 만들면서, 아직 피드백 받을 수 있는 상태에도 못 갔으니, 뭐가 아집인지, 킥인지 구별이 쉽지 않다.
흩어져 있는 가족끼리 일상을 기록하거나, 장소에 딸린 음악 기록, 낚시터 공유, 여행 루트 공유 등... 분명 쓰임새는 보여서, 여기서 그만 두기에는 아쉽다.