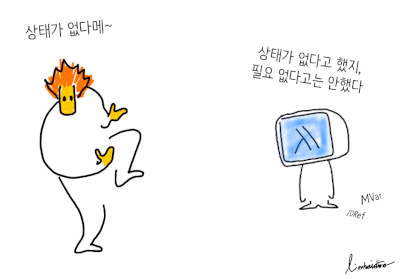
무려 4년 전에 패터슨 조건을 공부하고 정리 해 놨는데, 패터슨 조건이란 말을 보고, "어, 저거 어디서 들어 본 건데..."하고 있다. 입력이 누적되지 않고, 점점 밑 빠진 독처럼 새 나간다... 씁쓸하네...이거.
lionhairdino
@lionhairdino@hackers.pub · 34 following · 33 followers
I run a blog on the topic of the Haskell language, mainly covering functional programming and Haskell-related discussions. If someone talks about these topics, I act like we're old friends, even if it's our first time meeting.
해커스펍에서 댓글을 달 때, 굳이 @로 아이디 언급을 하지 않아도, 원 글과 타래는 연관 지어지는 거지요? 타래에 참여하고 있는 분들이 여럿이라면, 다 언급을 해야 하는 거고, 한 분이라면 굳이 언급하지 않아도 되는 거고요?
![]() @lionhairdino
@lionhairdino ![]() @bglbgl gwyng 어느 쪽이 더 "정상이다"가 아니라, GADTs의 Record 갱신을 지원하려면 필요한 변경입니다.
@bglbgl gwyng 어느 쪽이 더 "정상이다"가 아니라, GADTs의 Record 갱신을 지원하려면 필요한 변경입니다.
9.6 전에는 실수로 허용되던 것이란 말이 나와, 학문적 정 부 의 가치가 있는 줄 알았습니다. ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4) ![]() @bglbgl gwyng
@bglbgl gwyng
답 댓글이 아니라, 질문 댓글입니다. 레코드 업데이트 하는 동안에 반드시 레코드 타입을 먼저 알아야 한다는 게 "정상"이라는 거지요?
bar :: T Int
-- bar = emptyT --- 허용
bar = emptyT { x = [3] } --- 레코드 업데이트 중에는 타입 specialize를 못하니 불가컴파일러 변화가 하나만 있다해서, 하나가 아닌데 하고 댓 달았는데, 읽어보니 다나 마나한 댓을 달았네요. 마이그레이션 페이지에 있는 내용을 풀어서 설명하신 거였군요. ![]() @bglbgl gwyng
@bglbgl gwyng
https://gitlab.haskell.org/ghc/ghc/-/wikis/migration/9.6#superclass-expansion-is-more-conservative
내가 9.4 -> 9.6 마이그레이션에서 겪고 있는 문제가 이거랑 관련이 있는거 같은데(확실치 않음)... 9.4에서는 c :: Type -> Constraint 일때 forall c. c Int 뭐 이런 조건이 있으면, 모든 c에 대해 c Int가 존재하는게 말이 안되는데도 실제로 c Int 꼴로 쓰이는 c만 고려해서 타입체크를 통과시켜줬던거 같다(이것도 확실하지 않음). 근데 9.6에선 당연히 거부당한다.
위의 내 이해가 맞다면 9.4의 constraint solving 완전 무근본이었단건데, 이건 또 믿기 어렵다(하스켈의 설계 결정에 대한 신뢰 유지한다고 하면). 어디서 내가 잘못 파악한거지.
9.6 migration 컴파일러 변화가 타입 패밀리, 슈퍼 클래스 관련 동작이 있네요. ![]() @bglbgl gwyng
@bglbgl gwyng
3년차 웹 프런트엔드 개발자입니다. 잠시 10주 여름 방학 동안 계약직으로 일할 수 있는 직장을 찾고 있습니다. (6월 마지막 주부터 8월 마지막 주) http://frontend.moe/portfolio/
올해 2학기까지 수료하면 졸업 예정이라, 학부 졸업 이후 정규직 전환 조건으로도 희망하고 있습니다.
하스켈 학교 운영자!
어디까지나 재미로 쌍대dual을 이해하기 위한 훈련을 하고 있습니다.
(※ 리스트는 []에서 extract할 게 없어 모나드의 쌍대인 코모나드가 정의되지 않아 NonEmpty 타입으로 테스트 했습니다.)
λ> join $ (1:|[2]):|[3:|[4]]
1 :| [2,3,4]
λ> duplicate $ 1:|[2,3]
(1 :| [2,3]) :| [2 :| [3],3 :| []]
λ> join $ duplicate $ 1:|[2,3]
1 :| [2,3,2,3,3]duplicate :: w a -> w (w a)와 join :: m (m a) -> m a를 연속으로 하면 처음 구조로는 돌아 오지만, 완전히 값까지 같은 상태로 돌아 오진 않습니다.
(완벽히 같은 곳으로 돌아오는 걸 역inverse이라 부르고, 역인 관계 두 연산을 합치면 id가 됩니다. Not처럼 역이 듀얼인 경우도 있습니다.)
("우편물 발송, 수취는 듀얼 관계지만, 뭘 보내고 받았는지까지 보는 건 아니다." 비유와 맞을지 모르겠습니다.)
"미래는 코모나드적이다"란 말을 만나곤 하는데, 이는 미래는 어차피 과거 조합으로 정해질 수 있는 모양 중 하나란 뜻으로 보입니다.
재미로, 모나드와 코모나드 비교를 한 문장으로 표현하면,
“모나드의 미래는 알 수 없지만, 코모나드의 과거는 지금을 만들 수 있었던 정해진 경우의 수들이다.”
고정된 환경값 하나를 넣어주는 Reader 모나드는, 즉 매 번 이펙트가 똑같다면, 과거나 미래나 같으니, 모나드와 코모나드의 동작이 같게 나오는 걸로 보입니다.
그래서, 최종 쌍대dual를 비전공자의 교양 수준의 말로, 최대한 똑 떨어지게 설명하면, 구조를 반대로 뒤집어도 성립하는 대칭성이다.
![]() @ailrunAilrun (UTC-5/-4) 님 설명 참고: "쌍대란 쌍대의 쌍대가 자기 원래의 대상과 같은 무언가"
@ailrunAilrun (UTC-5/-4) 님 설명 참고: "쌍대란 쌍대의 쌍대가 자기 원래의 대상과 같은 무언가"
![]() @lionhairdino 쌍대는 너무 일반적인 개념이라 쌍대 자체를 응용하기에는 구체성이 모자라고요, 어떤 것의 쌍대를 이용할 것인가를 살펴봐야지요. 이를테면
@lionhairdino 쌍대는 너무 일반적인 개념이라 쌍대 자체를 응용하기에는 구체성이 모자라고요, 어떤 것의 쌍대를 이용할 것인가를 살펴봐야지요. 이를테면 A의 쌍대를 A -> Void로 생각할 때에는 쌍대의 쌍대가 (A -> Void) -> Void, 즉 Continuation Passing Style에 해당하는 변환을 주지요.
와, 더 마법스러워 보입니다. 내재된 근본 원리를 어찌 이해해야 저렇게 응용해야지 하는 생각이 들까요. (질문 아니고 감탄입니다.) ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
![]() @lionhairdino 두 번 취해서 제자리로 돌아와야하니 +1을 -1로 보내고 -1을 +1로 보내는 것에 더 가깝지요
@lionhairdino 두 번 취해서 제자리로 돌아와야하니 +1을 -1로 보내고 -1을 +1로 보내는 것에 더 가깝지요
adjoint도 두 개가 짝을 이뤄 뭔가를 완성하는 느낌이 있었는데, dual도 뭔가 시스템이 완성?안정?된 느낌도 들고 그러네요.
아직 콕 짚지는 못하지만, 프로그램 설계할 때, 기계적으로 따르기만 해도 도움이 될 것 같은 요소가 있을 것만 같아서, 가끔 이해하고 싶은 욕구가 생기는데, "화살표를 싹다 뒤집으면 듀얼"이야 같은 말로는 응용할 수 있을만한 이해에 도달을 못하고 있습니다.
인문학스런 해석 질문은 그만 드려야겠지요. ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
![]() @lionhairdino 그나마 나은 설명은 "쌍대란 쌍대의 쌍대가 자기 원래의 대상과 같은 무언가" 아닐까요.
@lionhairdino 그나마 나은 설명은 "쌍대란 쌍대의 쌍대가 자기 원래의 대상과 같은 무언가" 아닐까요.
아하!하고 답 달려고 고민했는데, 역시나 어렵네요. 둘이 서로 반쪽같은 것들로, 둘을 가지고 있으면 뭔가 되는 그런 "느낌"이라고 뿐이 감이 안오네요. 0에서 +1로 갔다가 -1로 오면 "역"이지만, 0에서 +1로 가고, 0에서 -1로 가는 건 듀얼로 볼 수 있겠지요? 똑 떨어지지 않는 인문학 같아요. ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
아, 얘가 절 알아버렸네요. 어찌 알았지. 프롬프트 히스토리 어딘가에 있나...
물리학자들은 1시간에 못 고칠 겁니다. 그들은 잘 하는 게 프로그래밍이 아닐거에요. 못하는 사람들을 너무 미워하지 마세요. ![]() @bglbgl gwyng
@bglbgl gwyng
제가 못해서 욕먹은 경험이 있어 편드는 거 아닙니다 ;-) ![]() @bglbgl gwyng
@bglbgl gwyng
적용을 주목해서 보면
a->b, b->c 합성의 구현은 a에 a->b를 적용 $의 체이닝으로 볼 수 있다.
b->c $ a->b $ id a
λ> (+1) $ (+2) $ 3a->mb, b->mc 합성은 ma에 a->mb를 적용 >>=의 체이닝
return a >>= a->mb >>= b->mc
λ> Just 3 >>= (\x -> Just (x+1)) >>= (\x -> Just (x+2))wa->b, wb->c 합성은 wa->b를 wa에 적용 extend의 체이닝
wb->c extend (wa->b extend duplicate wa)
λ> (\(Identity x) -> x+1) `extend` (\(Identity x) -> x+2) (duplicate (Identity 3))이런 눈으로 보면, Functor 적용 <$>, Applicatives 적용<*>(이 둘은 다른 결에 있긴 하지만) 등 이 덜 낯설게 보인다.
(코모나드 정리 노트 중 일부입니다.)
![]() @lionhairdino 제가 한건 기초적인 수정이라 거기에 대해 큰 보상을 바라진 않습니다. 반대로, 치킨먹으며 1시간이면 고칠 문제를 오랫동안 방치한 그 팀의 물리학자들에게 응당의 처벌이 가해지기를 바랍니다.
@lionhairdino 제가 한건 기초적인 수정이라 거기에 대해 큰 보상을 바라진 않습니다. 반대로, 치킨먹으며 1시간이면 고칠 문제를 오랫동안 방치한 그 팀의 물리학자들에게 응당의 처벌이 가해지기를 바랍니다.
물리학자들은 1시간에 못 고칠 겁니다. 그들은 잘 하는 게 프로그래밍이 아닐거에요. 못하는 사람들을 너무 미워하지 마세요. ![]() @bglbgl gwyng
@bglbgl gwyng
어허, 꼬리 치는게 예사롭지 않네요. 홀리겠는데요.
“자고 일어나서 마저 해야지!” 하고 자고 일어났는데 어디까지 했고 뭘 해야 하는지 다 까먹었다.
혹시 자야되는 때를 넘긴 것 아닌가요? 졸음을 참고 작업하면 어떤식으로든 탈이 나는 경험을 자주하고 나니, 이제 졸리면 잡니다. 세상 안무너진다하고.ㅎㅎ ![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)
친구가 외국 반도체회사에 다니는데 이름만 들으면 다 아는 세계에서 손꼽히는 회사다. 1년 전쯤에, 친구가 자기 팀에서 예전부터 쓰고있는 시뮬레이션 코드가 너무 복잡해서 리팩토링 하고 싶다고 나를 찾아왔다. 한 2, 3000줄 되는 Numpy 코드였다.
나는 시뮬레이션의 의미 자체는 전혀 이해를 못하니(이래서 보안문제도 익스큐즈 할수 있었을 것이다), 그냥 코드의 모양만 보고 이상한 부분을 조금씩 고쳐나갔다. 그... 전형적인 물리학자들의 실험실 코드였다(코드를 못짜는건 이해를 하는데, 거기에 대해 한치의 부끄러움도 느끼지 않는다는 점이 뒷목을 잡게 만든다). Numpy 함수도 제대로 활용을 못해놨길래, 나도 Numpy 잘 못쓰지만 대충 이런 함수가 아마 있겠지... 하고 검색해서 찾아내서 교체하고 이런걸 반복했다.
이것저것 고친 다음에 잘돌아가나 한번 실행을 해봤는데, 이럴수가. 시뮬레이션이 1000배 빨라졌다. 아니 뭐, 한 2배 3배 빨라졌으면 내 솜씨라고 자부할텐데, 1000배 빨라진거는 그냥 원래 코드가 똥통이었다고 해석할수 밖에 없다. 구라안치고 정말 1000배다. 1000배의 성능향상의 보답으로 나는 교촌치킨웨지콤보세트를 현장에서 받아먹었다.
그 이후에 어떤 일이 있었냐. 기존 시뮬레이션 코드로는 하루에 시뮬레이션을 2, 3번정도밖에 돌리지 못했는데, 1000배 빨라지고 나니까 결과가 수십초만에 나오니 하루에 수백번 돌릴수 있게 된것이다(내가 고친 코드가 전부는 아니어서 1000배 향상은 아닌데, 가장 큰 병목이긴 해서 결국 100배 이상이라는 듯). 그때부터 100배 많아진 데이터를 처리하기 위한 인프라가 필요해졌다. 그래서 거기 개발팀이 데이터베이스와 데이터 파이프라인 구축을 시작하게 되었다고 한다. 그 팀에서는 일종의 특이점이 시작된것이다;;
결론: 교촌치킨웨지콤보 세트는 개맛있었다.
한 사람의 안목이 큰 이득으로 돌아 올 때, 정당한 대우에 대한 고민이 듭니다. 구름빵 라이센스가 생각납니다. 누군가 옆에서 그럴 겁니다. 교촌 세트 두 번은 먹어야지!? ![]() @bglbgl gwyng
@bglbgl gwyng
듀얼은 일반인이 이해하게, 간단한 문장으로 똑 떨어지게 설명하기 어렵네요 (관련 전공자 아님)
@jasonkim자손킴 어서오세요~~
![]() lionhairdino replied to the below article:
lionhairdino replied to the below article:
함수형 언어의 평가와 선택
Ailrun (UTC-5/-4) @ailrun@hackers.pub
함수형 언어(Functional Language)의 핵심
함수형 언어가 점점 많은 매체에 노출되고, 더 많은 언어들이 함수형 언어의 특징을 하나 둘 받아들이고 있다. 함수형 언어, 적어도 그 특징이 점점 대세가 되고 있다는 이야기이다. 하지만, 함수형 언어가 대체 무엇이란 말인가? 무엇인지도 모르는 것이 대세가 된다고 할 수는 없지 않은가?
함수형 언어란 아주 단순히 말해서 함수가 표현식[1]인 언어를 말한다. 다른 말로는 함수가 값이기 때문에 다른 함수를 호출해서 함수를 얻어내거나 함수의 인자로 함수를 넘길 수 있는 언어를 말한다. 그렇다면 이 단순화된 핵심만을 포함하는 언어로 함수형 언어의 핵심을 이해할 수 있지 않을까? 이게 바로 람다 대수(Lambda Calculus)의 역할이다.[2]
람다 대수는 딱 세 종류의 표현식만을 가지고 있다.
- 변수 (xx, yy, …\ldots)
- 매개변수 xx에 인자를 받아 한 표현식 MM(함수의 몸체)을 계산하는 함수 (λx→M\lambda x\to M)
- 어떤 표현식 LL의 결과 함수를 인자 NN으로 호출 (L NL\ N)
이후의 설명에서는 MM 과 NN, 그리고 LL이라는 이름을 임의의 표현식을 나타내기 위해 사용할 것이다. 람다 대수가 어떤 것들을 표현할 수 있는가? 앞에서 말했듯이 람다 대수는 함수의 인자와 함수 호출의 결과가 모두 함수인 표현식을 포함한다. 예를 들어 λx→(λy→y)\lambda x \to (\lambda y \to y) 는 매개변수 xx에 인자를 받아 함수 λy→y\lambda y \to y를 되돌려주는 함수이고, λx→(x (λy→y))\lambda x \to (x\ (\lambda y \to y))는 매개변수 xx에 함수인 인자를 받아 그 함수를 (λy→y\lambda y \to y를 인자로 사용하여) 호출하는 함수이다.
람다 대수(Lambda Calculus)의 평가(Evaluation)
이제 문제는
그래서 람다 대수의 표현식이 하는 일이 뭔데?
이다. 위의 표현식에 대한 소개는 산수로 말하자면 x+yx + y와 같이 연산자(++)와 연산항(xx와 yy)로부터 얻어지는 문법만을 설명하고 있고, 3+53 + 5와 같은 구체적인 표현식을 계산해서 88이라는 결과 값을 내놓는 방식을 설명하고 있지 않다. 이런 표현식으로부터 값을 얻어내는 것을 언어의 "평가 절차"("Evaluation Procedure")라고 한다. 람다 대수의 평가 절차를 설명하는 것은 어렵지 않다. 적어도 표면적으로는 말이다.
- 함수는 이미 값이다.
- 함수 λx→M\lambda x \to M을 NN으로 호출하면 MM에 등장하는 모든 xx을 NN으로 치환(Substitute)하고 결과 표현식의 평가를 계속한다.
이는 겉으로 보기에는 말이 되는 설명처럼 보인다. 하지만 이 설명을 실제로 해석기(Interpreter)로 구현하려고 시도한다면 이 설명이 사실 여러 세부사항을 무시하고 있다는 점을 깨닫게 될 것이다.
- 함수 호출 L NL\ N에서 LL이 (아직) λx→M\lambda x \to M 꼴이 아닐 때는 어떻게 해야하지?
- 함수 호출 (λx→M) N(\lambda x \to M)\ N에서 NN을 먼저 평가하는 게 낫지 않나? xx가 MM에 여러번 등장한다면 NN을 여러번 평가해야 할텐데?
첫번째 문제는 비교적 간단히 해결할 수 있다. LL을 먼저 평가해서 λx→M\lambda x \to M 꼴의 결과 값을 얻어낸 뒤에 호출을 실행하면 되기 때문이다. 반면에 두번째 질문은 좀 더 미묘한 문제를 가지고 있다. 함수 호출의 평가에서 발생하는 이 문제에 구체적인 답을 하기 위해서는 값에 의한 호출(Call-By-Value, CBV)와 이름에 의한 호출(Call-By-Name, CBN)이 무엇인지 이해해야 한다.
값에 의한 호출(Call-By-Value)? 이름에 의한 호출(Call-By-Name)?
앞에서 말한 함수 호출에서부터 발생하는 문제는 사실 함수형 언어에서만 발생하는 문제는 아니다. C와 같은 명령형 언어에서도 함수를 호출할 때 인자를 먼저 평가해야하는지를 결정해야하기 때문이다. 즉 이 문제는 함수를 가지고 있고 함수를 호출해야하는 모든 언어들이 가지고 있는 문제이다.
그렇다면 이 일반적인 문제를 어떻게 해결하는가? 대부분의 언어가 취하는 가장 대표적인 방식은 "값에 의한 호출"("Call-By-Value", "CBV")이라고 한다. 이 함수 호출 평가 절차에서는 함수의 몸체에 인자를 치환하기 전에[3] 인자를 먼저 평가한다. 이 방식을 사용하면 인자를 여러번 평가해야하는 상황을 피할 수 있다.
또 다른 방식은 "이름에 의한 호출"("Call-By-Name", "CBN")이라고 한다. 이 방식에서는 함수의 몸체에 인자를 우선 치환한 후 몸체를 평가한다. 몇몇 언어의 매크로(Macro)와 같은 기능이 이 방식을 사용한다. 얼핏 보기에는 CBN은 장점이 없어보인다. 그러나 함수가 인자를 사용하지 않을 경우는 CBN이 장점을 가진다는 것을 볼 수 있다. 극단적으로 평가가 종료되지 않는 표현식(Non-terminating expression)이 있다면[4] CBV는 종료하지 않고 CBN만이 종료하는 경우가 있음을 다음 예시를 통해 살펴보자. 표현식 (λx→(λy→y)) N(\lambda x \to (\lambda y \to y))\ N이 있다고 할 때, NN이 평가가 종료되지 않는 표현식이라고 하자. 이 경우 CBV를 따른다면 종료하지 않는 NN 평가를 먼저 수행하느라 이 표현식의 값을 얻어낼 수 없지만, CBN을 따른다면 λy→y\lambda y \to y라는 값을 손쉽게 얻어낼 수 있다. 바로 이런 상황 때문에
CBN은 CBV보다 일반적으로 더 많은 표현식들을 평가할 수 있다
고 말한다.
모호한 선택을 피하는 방법
두 방식의 장점을 모두 가질 수는 없을까? 다시 말해서, 어떤 상황에서는 이름에 의한 호출을 사용하고, 어떤 상황에서는 값에 의한 호출을 사용할 수 없을까? 이 질문에 답한 수많은 선구자들 가운데 폴 블레인 레비(Paul Blain Levy)가 내놓은 답인 "값 밀기에 의한 호출"("Call-By-Push-Value", "CBPV")은 함수형 언어의 평가를 기계 수준(Machine level)에서 이해하는데에 있어 강력한 도구를 제공한다. CBPV는 우선 "계산"("Computation")과 "값"("Value")을 구분한다.
- 계산 MM, NN, LL, …\ldots = 함수 λx→M\lambda x \to M 또는 함수 호출 L VL\ V
- 값 VV, UU, WW, …\ldots = 변수 xx
잠깐, 앞서서 함수형 언어에서 함수는 값이라고 하지 않았던가? 이는 값 밀기에 의한 호출에서 함수와 함수 호출을 종전과 전혀 다르게 이해하기 때문이다. 함수 λx→M\lambda x \to M는 스택(Stack)에서 값을 빼내어(Pop) xx라는 이름을 붙인 후 MM을 평가하는 것이고, 함수 호출 L VL\ V는 스택에 값 VV를 밀어넣고(Push)[5] LL을 평가하는 것이다. 따라서 함수 λx→M\lambda x \to M는 평가의 결과가 아닌 추가적인 평가가 가능한 표현식이 된다. 이 구분을 간결하게 설명하는 것이 다음의 CBPV 표어이다.
값은 "~인 것"이다. 계산은 "~하는 것"이다.
그렇지만 함수형 언어이기 위해서는 함수를 값으로 취급할 수 있어야 한다고 했지 않은가? 그렇다. 이를 위해 CBPV는
계산을 강제한다면(force\mathbf{force}) 계산 MM를 하는 지연된 계산인 값 thunk(M)\mathbf{thunk}(M)
을 추가로 제공한다. 이 둘 (force(V)\mathbf{force}(V)와 thunk(M)\mathbf{thunk}(M))을 다음과 같이 문법에 추가할 수 있다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V)
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
CBPV를 완성하기 위해 필요한 마지막 조각은 계산을 끝내는 법이다. 현재까지 설명한 λx→M\lambda x \to M와 L VL\ V 그리고 force(V)\mathbf{force}(V) 는 모두 다음 계산을 이어서 하는 표현식이고, 계산을 끝내는 방법을 제공하지는 않는다. 예를 들어 λx→M\lambda x \to M의 평가는 스택에서 값을 빼내고 계산 MM의 평가를 이어한다. 그렇다면 계산의 끝은 무엇인가? 결과 값을 제공하는 것이다. 이를 위해 return(V)\mathbf{return}(V)를 계산에 추가하고, 이 결과 값을 사용할 수 있도록 M to x→NM\ \mathbf{to}\ x \to N (계산 MM을 평가한 결과 값을 xx라고 할 때 계산 NN을 평가하는 계산) 또한 계산에 추가하면 다음의 완성된 CBPV를 얻는다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V) 또는 return(V)\mathbf{return}(V) 또는 M to x→NM\ \mathtt{\mathbf{to}}\ x \to N
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
이제 CBPV를 얻었으니 원래의 목표로 돌아가보자. 어떻게 CBV 호출과 CBN 호출을 CBPV로 설명할 수 있을까?
- CBV 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 return(thunk(λx→M))\mathbf{return}{(\mathbf{thunk}(\lambda x \to M))}과 L to x→N to y→force(x) yL\ \mathbf{to}\ x \to N\ \mathbf{to}\ y \to \mathbf{force}(x)\ y로 표현할 수 있다. 즉, CBPV의 관점에서 CBV의 함수는 지연된 원래 계산 λx→M\lambda x \to M을 값으로 되돌려주는 계산으로 이해할 수 있고, 함수 호출 L NL\ N은 함수 부분 LL을 먼저 평가하고 NN을 평가한 뒤 NN의 계산 결과 yy를 스택에 밀어넣고 지연된 계산인 함수 부분 xx의 계산을 강제하는(force(x)\mathbf{force}(x)) 것으로 이해할 수 있다.
- CBN 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 λx→M\lambda x \to M(단, 변수 xx의 모든 사용을 force(x)\mathbf{force}(x)로 치환함)과 L thunk(N)L\ \mathbf{thunk}(N)로 표현할 수 있다. 즉, CBPV의 관점에서 함수 호출은 L NL\ N은 지연된 NN을 스택에 밀어넣은 뒤 LL의 계산을 이어가는 것으로 볼 수 있다. 이 지연된 NN은 이후에 스택에서 빼내어져 어떤 이름 xx가 붙은 뒤, 이 변수가 사용될 때에야 비로소 계산된다.
다소 설명이 복잡할 수 있으나, 단순하게 말해서 CBPV는 CBV에 따른 상세한 평가 순서와 CBN 따른 상세한 평가 순서를 세부적으로 설명할 수 있는 충분한 기능을 모두 갖추고 있으며, 이를 통해 CBV 함수 호출과 CBN 함수 호출을 모두 설명할 수 있다는 이야기이다.
기계 수준(Machine level)에서의 Call-By-Push-Value의 장점
앞에서는 CBPV가 CBV와 CBN를 모두 설명할 수 있음을 다뤘다. 그러나 CBPV는 프로그래머(Programmer)가 직접 사용하기에는 과도하게 자세한 세부사항들을 포함하고 있기에, 프로그래머가 직접 CBPV를 써서 CBV와 CBN의 구분을 조율하기에는 적합하지 않다. 그렇다면 어느 수준에서 CBV와 CBN을 혼합해 사용할 때 도움을 줄 수 있을까? 바로 람다 대수를 기계 수준으로 컴파일(Compile)할 때이다. 이때는 CBPV가 가진 자세한 세부사항의 표현력이 굉장히 유용해진다.
예를 들어 람다 대수를 기계 수준으로 변환할 때 흔히 필요한 것 중 하나인 항수 분석(Arity analysis)에 대해 이야기해보자. 항수 분석은 함수가 하나의 인자를 받은 뒤 실행되어야 하는지, 혹은 두 인자를 모두 받아 실행되어야 하는지 등을 확인하여 이후에 그에 걸맞는 최적화된 기계어(Machine language)를 생성할 수 있게 도와주는 분석 작업이다. 평범한 람다 대수에서는 항수 분석의 결과를 직접적으로 표현하기 어렵다. 예를 들어 람다 대수의 λx→(λy→y)\lambda x \to (\lambda y \to y)의 경우 이 함수가 xx와 yy를 모두 받아 yy를 되돌려주는 함수인지 (항수가 2인 함수인지), 혹은 xx를 받아 λy→y\lambda y \to y라는 함수를 되돌려주는 함수인지 (항수가 1인 함수인지) 구분할 수 없다. 그러나 이를 CBPV로 변환한 λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))나 λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 각각이 무엇을 뜻하는지 분명히 이해할 수 있다.
- λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))는 두 변수 xx와 yy를 스택에서 빼낸 뒤 yy의 값을 되돌려주는 함수(항수가 2인 함수)이다.
- λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 변수 xx를 스택에서 빼낸 뒤 지연된 계산 λy→return(y)\lambda y \to \mathtt{return}(y)를 돌려주는 함수(항수가 1인 함수)이다.
이런 장점을 바탕으로 CBPV를 더 발전시킨 "언박싱한 값에 의한 호출"("Call-By-Unboxed-Value")을 GHC 컴파일러의 중간 언어(Intermediate language)로 구현하는 것에 대한 논의가 현재 진행되고 있으며 앞으로 더 많은 함수형 컴파일러들이 관련된 중간 언어를 채용하기 시작할 것으로 보인다.
마치며
이 글에서는 함수형 언어의 핵인 람다 대수를 간단히 설명하고 람다 대수를 평가하는 방법에 대해서 다루어보았다. 특히 그 중 값 밀기에 의한 평가(Call-By-Push-Value, CBPV)가 무엇이며 CBPV가 다른 대표적인 두 방법(CBV, CBN)을 어떻게 표현할 수 있는지, 그리고 CBPV의 장점이 무엇인지에 대해서도 다루어 보았다. 이 글에서 미처 다루지 못한 중요한 주제는 CBPV를 기계에 가까운 언어로 번역해보는 것이다. 여기에서는 글이 너무 복잡해지는 것을 피하기 위해 제했으나, CBPV의 장점에서 살펴봤듯 이는 CBPV에 있어 핵심 주제 중 하나이기 때문에 이후에 다른 글을 통해서라도 이 주제를 소개할 기회를 가지고자 한다. 이 글이 CBPV에 대한 친절한 소개글이었기를 바라며 이만 줄이도록 하겠다.
결과 값(Value)을 가지는 언어 표현을 말한다. 예를 들어 1+11 + 1은 22라는 값을 가지는 표현식이지만 (JavaScript의)
let x = 3;나 (Python의)def f(): ...은 그 자체로는 값이 없기 때문에 표현식이 아니다. ↩︎다만 실제 역사에서는 람다 대수의 이해와 발견이 함수형 언어의 개발보다 먼저 이루어졌다. 이런 역사적 관점에서는 (이미 많은 수학자들이 이해하고 있던) 람다 대수에 여러 기능을 추가한 것이 바로 함수형 언어라고 볼 수 있다. ↩︎
프로그래밍 언어(Programming Language)는 실제로는 치환을 사용하지 않고 환경(Environment)을 사용하는 경우가 더 많지만 설명의 편의를 위해 다른 언어들 또한 환경 대신 치환에 기반해 평가한다고 가정하겠다. ↩︎
앞서 설명한 람다 대수에서는 이를 쉽게 얻을 수 있다. 오메가(Ω\Omega)라고 부르는 표현식인 (λx→x x) (λx→x x)(\lambda x \to x\ x)\ (\lambda x \to x\ x)의 평가는 값에 의한 호출을 따르든 이름에 의한 호출을 따르든 종료되지 않는다. ↩︎
바로 이 함수 호출을 값 밀기에 기반해 해석하는 데에서 CBPV의 이름이 유래했다. ↩︎
(비전공자가 볼 내용은 아닌 것 같긴 한데요.) 취미 공부하는 사람의 질문입니다.
"인자를 받는다"는 행위를
"인자를 스택에 넣는다" 와 "인자를 스택에서 빼낸다" 둘 로 쪼개어
보는 아이디어에서 시작하는 것으로 보면 되나요?
그래서 adjoint란 용어가 아른 거리는 건가 싶습니다.
람다식을, 인자가 아직 들어오지 않아 reduce할 게 없는 값으로 볼 때는
[1.인자를 스택에 push ---2.인자를 스택에서 pop] 이 없어 reduce할 게 없는 상태로 봤는데,
CBPN에선 [2.인자를 스택에서 pop]은 있고, 이 걸로 reduce할 게 있는 상태.
로 본다는 얘기인가요?
위 설명에서 질문하고 싶은 것도 한 가득이고, @domatdo도막도 님의 이어지는 질문도 어렵긴 한데, 뭔가 전부는 아니더라도 "제가 필요한 정도"의 것은 건져갈 게 보이는 것 같아 질문드립니다.
![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
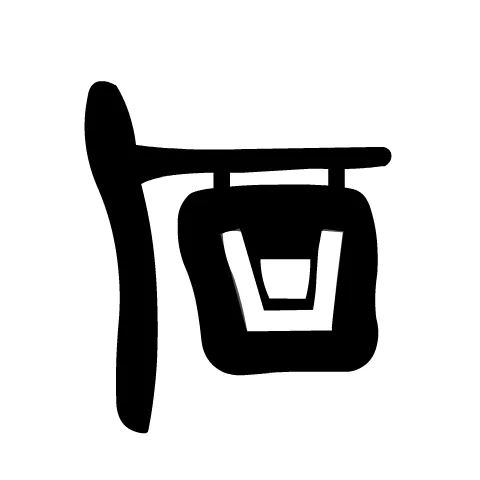
해커즈 퍼브의 favicon 이야기가 나왔을 때 잠깐 생각나는 대로 대충 낙서해 본 것이 있습니다. (말 그대로 대충 낙서입니다. 이대로 쓰자는 뜻은 아닙니다. 너무 진지하게 받아들이지는 마시고, 브레인스토밍 정도로 생각해 주시길...)
- 퍼브 간판의 일반적인 형상을 가져왔습니다.
- 마실 것을 파는 장소의 간판 같은 느낌을 유지하면서, 정확히 어떤 음료인지는 의도적으로 알 수 없게 했습니다. ("퍼브"는 맥주를 주력으로 하는 장소라는 인식이 있는 것 같습니다만, 법적·의료적·종교적 여러 가지 이유로 알코올을 음용할 수 없는 사람들이 세상에는 아주 많기 때문에, 일부러 "맥주"의 이미지를 배제했습니다. 해커즈 퍼브는 술 안/못 마시는 사람도 편하게 올 수 있는 장소가 되는 것이, 행동 강령의 취지에도 부합한다는 생각이었습니다.)
- 간판 부분은 잘 보시면 "퍼브"라는 한글 표기에서 "ㅍ"와 "ㅂ"를 담고 있습니다. 가로대와 간판이 이어지는 부분이 "ㅍ"의 형상이고, 물잔이 "ㅂ"의 형상입니다. 물론 해커즈 퍼브는 한국어 전용 커뮤니티도 아니고 한글 전용 커뮤니티는 더더욱 아닙니다. 한글이 꼭 들어가야 할 이유는 없습니다. 하지만 반대로 한글을 안 쓸 이유도 없지 않은가? 뭔가를 모티브로 쓰긴 써야 하는데 그게 한글일 수도 있는 것 아닌가? 그래서 넣어 봤습니다. 😅
- "Hacker's Pub"를 구성하는 글자들을 그대로 집어넣는 것을 일부러 피했습니다. 우선, 아이콘은 "Hackers' Pub"이라는 텍스트와 병치될 가능성이 높은데, 그렇다면 "H"나 "P"가 들어 있는 것은 중복이 되고 정보 전달의 낭비가 됩니다. 그리고, favicon 으로 쓰일 가능성이 높은데, 다른 사이트들에도 알파벳을 형상화한 아이콘이 많습니다. 추상적 형상으로서 다른 아이콘들과 겹칠 여지가 적을수록 식별자로서의 기능과 효용이 극대화될 것이라는 생각이었습니다. (물론, 엄밀히 따지면, 이 아이콘도 전체 형상에는 알파벳 "h"의 구조가 숨어 있고, 그것을 의도하긴 했습니다만, 가장 먼저 눈에 들어오는 특징은 아니죠.)
해커스 퍼브보다는 해커스 주막!이 떠오릅니다. 숨은 디자인 의도들도 다 의미가 있고 멋진데요.@xtjuxtapose
![]() lionhairdino shared the below article:
lionhairdino shared the below article:
함수형 언어의 평가와 선택
Ailrun (UTC-5/-4) @ailrun@hackers.pub
함수형 언어(Functional Language)의 핵심
함수형 언어가 점점 많은 매체에 노출되고, 더 많은 언어들이 함수형 언어의 특징을 하나 둘 받아들이고 있다. 함수형 언어, 적어도 그 특징이 점점 대세가 되고 있다는 이야기이다. 하지만, 함수형 언어가 대체 무엇이란 말인가? 무엇인지도 모르는 것이 대세가 된다고 할 수는 없지 않은가?
함수형 언어란 아주 단순히 말해서 함수가 표현식[1]인 언어를 말한다. 다른 말로는 함수가 값이기 때문에 다른 함수를 호출해서 함수를 얻어내거나 함수의 인자로 함수를 넘길 수 있는 언어를 말한다. 그렇다면 이 단순화된 핵심만을 포함하는 언어로 함수형 언어의 핵심을 이해할 수 있지 않을까? 이게 바로 람다 대수(Lambda Calculus)의 역할이다.[2]
람다 대수는 딱 세 종류의 표현식만을 가지고 있다.
- 변수 (xx, yy, …\ldots)
- 매개변수 xx에 인자를 받아 한 표현식 MM(함수의 몸체)을 계산하는 함수 (λx→M\lambda x\to M)
- 어떤 표현식 LL의 결과 함수를 인자 NN으로 호출 (L NL\ N)
이후의 설명에서는 MM 과 NN, 그리고 LL이라는 이름을 임의의 표현식을 나타내기 위해 사용할 것이다. 람다 대수가 어떤 것들을 표현할 수 있는가? 앞에서 말했듯이 람다 대수는 함수의 인자와 함수 호출의 결과가 모두 함수인 표현식을 포함한다. 예를 들어 λx→(λy→y)\lambda x \to (\lambda y \to y) 는 매개변수 xx에 인자를 받아 함수 λy→y\lambda y \to y를 되돌려주는 함수이고, λx→(x (λy→y))\lambda x \to (x\ (\lambda y \to y))는 매개변수 xx에 함수인 인자를 받아 그 함수를 (λy→y\lambda y \to y를 인자로 사용하여) 호출하는 함수이다.
람다 대수(Lambda Calculus)의 평가(Evaluation)
이제 문제는
그래서 람다 대수의 표현식이 하는 일이 뭔데?
이다. 위의 표현식에 대한 소개는 산수로 말하자면 x+yx + y와 같이 연산자(++)와 연산항(xx와 yy)로부터 얻어지는 문법만을 설명하고 있고, 3+53 + 5와 같은 구체적인 표현식을 계산해서 88이라는 결과 값을 내놓는 방식을 설명하고 있지 않다. 이런 표현식으로부터 값을 얻어내는 것을 언어의 "평가 절차"("Evaluation Procedure")라고 한다. 람다 대수의 평가 절차를 설명하는 것은 어렵지 않다. 적어도 표면적으로는 말이다.
- 함수는 이미 값이다.
- 함수 λx→M\lambda x \to M을 NN으로 호출하면 MM에 등장하는 모든 xx을 NN으로 치환(Substitute)하고 결과 표현식의 평가를 계속한다.
이는 겉으로 보기에는 말이 되는 설명처럼 보인다. 하지만 이 설명을 실제로 해석기(Interpreter)로 구현하려고 시도한다면 이 설명이 사실 여러 세부사항을 무시하고 있다는 점을 깨닫게 될 것이다.
- 함수 호출 L NL\ N에서 LL이 (아직) λx→M\lambda x \to M 꼴이 아닐 때는 어떻게 해야하지?
- 함수 호출 (λx→M) N(\lambda x \to M)\ N에서 NN을 먼저 평가하는 게 낫지 않나? xx가 MM에 여러번 등장한다면 NN을 여러번 평가해야 할텐데?
첫번째 문제는 비교적 간단히 해결할 수 있다. LL을 먼저 평가해서 λx→M\lambda x \to M 꼴의 결과 값을 얻어낸 뒤에 호출을 실행하면 되기 때문이다. 반면에 두번째 질문은 좀 더 미묘한 문제를 가지고 있다. 함수 호출의 평가에서 발생하는 이 문제에 구체적인 답을 하기 위해서는 값에 의한 호출(Call-By-Value, CBV)와 이름에 의한 호출(Call-By-Name, CBN)이 무엇인지 이해해야 한다.
값에 의한 호출(Call-By-Value)? 이름에 의한 호출(Call-By-Name)?
앞에서 말한 함수 호출에서부터 발생하는 문제는 사실 함수형 언어에서만 발생하는 문제는 아니다. C와 같은 명령형 언어에서도 함수를 호출할 때 인자를 먼저 평가해야하는지를 결정해야하기 때문이다. 즉 이 문제는 함수를 가지고 있고 함수를 호출해야하는 모든 언어들이 가지고 있는 문제이다.
그렇다면 이 일반적인 문제를 어떻게 해결하는가? 대부분의 언어가 취하는 가장 대표적인 방식은 "값에 의한 호출"("Call-By-Value", "CBV")이라고 한다. 이 함수 호출 평가 절차에서는 함수의 몸체에 인자를 치환하기 전에[3] 인자를 먼저 평가한다. 이 방식을 사용하면 인자를 여러번 평가해야하는 상황을 피할 수 있다.
또 다른 방식은 "이름에 의한 호출"("Call-By-Name", "CBN")이라고 한다. 이 방식에서는 함수의 몸체에 인자를 우선 치환한 후 몸체를 평가한다. 몇몇 언어의 매크로(Macro)와 같은 기능이 이 방식을 사용한다. 얼핏 보기에는 CBN은 장점이 없어보인다. 그러나 함수가 인자를 사용하지 않을 경우는 CBN이 장점을 가진다는 것을 볼 수 있다. 극단적으로 평가가 종료되지 않는 표현식(Non-terminating expression)이 있다면[4] CBV는 종료하지 않고 CBN만이 종료하는 경우가 있음을 다음 예시를 통해 살펴보자. 표현식 (λx→(λy→y)) N(\lambda x \to (\lambda y \to y))\ N이 있다고 할 때, NN이 평가가 종료되지 않는 표현식이라고 하자. 이 경우 CBV를 따른다면 종료하지 않는 NN 평가를 먼저 수행하느라 이 표현식의 값을 얻어낼 수 없지만, CBN을 따른다면 λy→y\lambda y \to y라는 값을 손쉽게 얻어낼 수 있다. 바로 이런 상황 때문에
CBN은 CBV보다 일반적으로 더 많은 표현식들을 평가할 수 있다
고 말한다.
모호한 선택을 피하는 방법
두 방식의 장점을 모두 가질 수는 없을까? 다시 말해서, 어떤 상황에서는 이름에 의한 호출을 사용하고, 어떤 상황에서는 값에 의한 호출을 사용할 수 없을까? 이 질문에 답한 수많은 선구자들 가운데 폴 블레인 레비(Paul Blain Levy)가 내놓은 답인 "값 밀기에 의한 호출"("Call-By-Push-Value", "CBPV")은 함수형 언어의 평가를 기계 수준(Machine level)에서 이해하는데에 있어 강력한 도구를 제공한다. CBPV는 우선 "계산"("Computation")과 "값"("Value")을 구분한다.
- 계산 MM, NN, LL, …\ldots = 함수 λx→M\lambda x \to M 또는 함수 호출 L VL\ V
- 값 VV, UU, WW, …\ldots = 변수 xx
잠깐, 앞서서 함수형 언어에서 함수는 값이라고 하지 않았던가? 이는 값 밀기에 의한 호출에서 함수와 함수 호출을 종전과 전혀 다르게 이해하기 때문이다. 함수 λx→M\lambda x \to M는 스택(Stack)에서 값을 빼내어(Pop) xx라는 이름을 붙인 후 MM을 평가하는 것이고, 함수 호출 L VL\ V는 스택에 값 VV를 밀어넣고(Push)[5] LL을 평가하는 것이다. 따라서 함수 λx→M\lambda x \to M는 평가의 결과가 아닌 추가적인 평가가 가능한 표현식이 된다. 이 구분을 간결하게 설명하는 것이 다음의 CBPV 표어이다.
값은 "~인 것"이다. 계산은 "~하는 것"이다.
그렇지만 함수형 언어이기 위해서는 함수를 값으로 취급할 수 있어야 한다고 했지 않은가? 그렇다. 이를 위해 CBPV는
계산을 강제한다면(force\mathbf{force}) 계산 MM를 하는 지연된 계산인 값 thunk(M)\mathbf{thunk}(M)
을 추가로 제공한다. 이 둘 (force(V)\mathbf{force}(V)와 thunk(M)\mathbf{thunk}(M))을 다음과 같이 문법에 추가할 수 있다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V)
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
CBPV를 완성하기 위해 필요한 마지막 조각은 계산을 끝내는 법이다. 현재까지 설명한 λx→M\lambda x \to M와 L VL\ V 그리고 force(V)\mathbf{force}(V) 는 모두 다음 계산을 이어서 하는 표현식이고, 계산을 끝내는 방법을 제공하지는 않는다. 예를 들어 λx→M\lambda x \to M의 평가는 스택에서 값을 빼내고 계산 MM의 평가를 이어한다. 그렇다면 계산의 끝은 무엇인가? 결과 값을 제공하는 것이다. 이를 위해 return(V)\mathbf{return}(V)를 계산에 추가하고, 이 결과 값을 사용할 수 있도록 M to x→NM\ \mathbf{to}\ x \to N (계산 MM을 평가한 결과 값을 xx라고 할 때 계산 NN을 평가하는 계산) 또한 계산에 추가하면 다음의 완성된 CBPV를 얻는다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V) 또는 return(V)\mathbf{return}(V) 또는 M to x→NM\ \mathtt{\mathbf{to}}\ x \to N
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
이제 CBPV를 얻었으니 원래의 목표로 돌아가보자. 어떻게 CBV 호출과 CBN 호출을 CBPV로 설명할 수 있을까?
- CBV 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 return(thunk(λx→M))\mathbf{return}{(\mathbf{thunk}(\lambda x \to M))}과 L to x→N to y→force(x) yL\ \mathbf{to}\ x \to N\ \mathbf{to}\ y \to \mathbf{force}(x)\ y로 표현할 수 있다. 즉, CBPV의 관점에서 CBV의 함수는 지연된 원래 계산 λx→M\lambda x \to M을 값으로 되돌려주는 계산으로 이해할 수 있고, 함수 호출 L NL\ N은 함수 부분 LL을 먼저 평가하고 NN을 평가한 뒤 NN의 계산 결과 yy를 스택에 밀어넣고 지연된 계산인 함수 부분 xx의 계산을 강제하는(force(x)\mathbf{force}(x)) 것으로 이해할 수 있다.
- CBN 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 λx→M\lambda x \to M(단, 변수 xx의 모든 사용을 force(x)\mathbf{force}(x)로 치환함)과 L thunk(N)L\ \mathbf{thunk}(N)로 표현할 수 있다. 즉, CBPV의 관점에서 함수 호출은 L NL\ N은 지연된 NN을 스택에 밀어넣은 뒤 LL의 계산을 이어가는 것으로 볼 수 있다. 이 지연된 NN은 이후에 스택에서 빼내어져 어떤 이름 xx가 붙은 뒤, 이 변수가 사용될 때에야 비로소 계산된다.
다소 설명이 복잡할 수 있으나, 단순하게 말해서 CBPV는 CBV에 따른 상세한 평가 순서와 CBN 따른 상세한 평가 순서를 세부적으로 설명할 수 있는 충분한 기능을 모두 갖추고 있으며, 이를 통해 CBV 함수 호출과 CBN 함수 호출을 모두 설명할 수 있다는 이야기이다.
기계 수준(Machine level)에서의 Call-By-Push-Value의 장점
앞에서는 CBPV가 CBV와 CBN를 모두 설명할 수 있음을 다뤘다. 그러나 CBPV는 프로그래머(Programmer)가 직접 사용하기에는 과도하게 자세한 세부사항들을 포함하고 있기에, 프로그래머가 직접 CBPV를 써서 CBV와 CBN의 구분을 조율하기에는 적합하지 않다. 그렇다면 어느 수준에서 CBV와 CBN을 혼합해 사용할 때 도움을 줄 수 있을까? 바로 람다 대수를 기계 수준으로 컴파일(Compile)할 때이다. 이때는 CBPV가 가진 자세한 세부사항의 표현력이 굉장히 유용해진다.
예를 들어 람다 대수를 기계 수준으로 변환할 때 흔히 필요한 것 중 하나인 항수 분석(Arity analysis)에 대해 이야기해보자. 항수 분석은 함수가 하나의 인자를 받은 뒤 실행되어야 하는지, 혹은 두 인자를 모두 받아 실행되어야 하는지 등을 확인하여 이후에 그에 걸맞는 최적화된 기계어(Machine language)를 생성할 수 있게 도와주는 분석 작업이다. 평범한 람다 대수에서는 항수 분석의 결과를 직접적으로 표현하기 어렵다. 예를 들어 람다 대수의 λx→(λy→y)\lambda x \to (\lambda y \to y)의 경우 이 함수가 xx와 yy를 모두 받아 yy를 되돌려주는 함수인지 (항수가 2인 함수인지), 혹은 xx를 받아 λy→y\lambda y \to y라는 함수를 되돌려주는 함수인지 (항수가 1인 함수인지) 구분할 수 없다. 그러나 이를 CBPV로 변환한 λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))나 λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 각각이 무엇을 뜻하는지 분명히 이해할 수 있다.
- λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))는 두 변수 xx와 yy를 스택에서 빼낸 뒤 yy의 값을 되돌려주는 함수(항수가 2인 함수)이다.
- λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 변수 xx를 스택에서 빼낸 뒤 지연된 계산 λy→return(y)\lambda y \to \mathtt{return}(y)를 돌려주는 함수(항수가 1인 함수)이다.
이런 장점을 바탕으로 CBPV를 더 발전시킨 "언박싱한 값에 의한 호출"("Call-By-Unboxed-Value")을 GHC 컴파일러의 중간 언어(Intermediate language)로 구현하는 것에 대한 논의가 현재 진행되고 있으며 앞으로 더 많은 함수형 컴파일러들이 관련된 중간 언어를 채용하기 시작할 것으로 보인다.
마치며
이 글에서는 함수형 언어의 핵인 람다 대수를 간단히 설명하고 람다 대수를 평가하는 방법에 대해서 다루어보았다. 특히 그 중 값 밀기에 의한 평가(Call-By-Push-Value, CBPV)가 무엇이며 CBPV가 다른 대표적인 두 방법(CBV, CBN)을 어떻게 표현할 수 있는지, 그리고 CBPV의 장점이 무엇인지에 대해서도 다루어 보았다. 이 글에서 미처 다루지 못한 중요한 주제는 CBPV를 기계에 가까운 언어로 번역해보는 것이다. 여기에서는 글이 너무 복잡해지는 것을 피하기 위해 제했으나, CBPV의 장점에서 살펴봤듯 이는 CBPV에 있어 핵심 주제 중 하나이기 때문에 이후에 다른 글을 통해서라도 이 주제를 소개할 기회를 가지고자 한다. 이 글이 CBPV에 대한 친절한 소개글이었기를 바라며 이만 줄이도록 하겠다.
결과 값(Value)을 가지는 언어 표현을 말한다. 예를 들어 1+11 + 1은 22라는 값을 가지는 표현식이지만 (JavaScript의)
let x = 3;나 (Python의)def f(): ...은 그 자체로는 값이 없기 때문에 표현식이 아니다. ↩︎다만 실제 역사에서는 람다 대수의 이해와 발견이 함수형 언어의 개발보다 먼저 이루어졌다. 이런 역사적 관점에서는 (이미 많은 수학자들이 이해하고 있던) 람다 대수에 여러 기능을 추가한 것이 바로 함수형 언어라고 볼 수 있다. ↩︎
프로그래밍 언어(Programming Language)는 실제로는 치환을 사용하지 않고 환경(Environment)을 사용하는 경우가 더 많지만 설명의 편의를 위해 다른 언어들 또한 환경 대신 치환에 기반해 평가한다고 가정하겠다. ↩︎
앞서 설명한 람다 대수에서는 이를 쉽게 얻을 수 있다. 오메가(Ω\Omega)라고 부르는 표현식인 (λx→x x) (λx→x x)(\lambda x \to x\ x)\ (\lambda x \to x\ x)의 평가는 값에 의한 호출을 따르든 이름에 의한 호출을 따르든 종료되지 않는다. ↩︎
바로 이 함수 호출을 값 밀기에 기반해 해석하는 데에서 CBPV의 이름이 유래했다. ↩︎
![]() 洪 民憙 (Hong Minhee) replied to the below article:
洪 民憙 (Hong Minhee) replied to the below article:
함수형 언어의 평가와 선택
Ailrun (UTC-5/-4) @ailrun@hackers.pub
함수형 언어(Functional Language)의 핵심
함수형 언어가 점점 많은 매체에 노출되고, 더 많은 언어들이 함수형 언어의 특징을 하나 둘 받아들이고 있다. 함수형 언어, 적어도 그 특징이 점점 대세가 되고 있다는 이야기이다. 하지만, 함수형 언어가 대체 무엇이란 말인가? 무엇인지도 모르는 것이 대세가 된다고 할 수는 없지 않은가?
함수형 언어란 아주 단순히 말해서 함수가 표현식[1]인 언어를 말한다. 다른 말로는 함수가 값이기 때문에 다른 함수를 호출해서 함수를 얻어내거나 함수의 인자로 함수를 넘길 수 있는 언어를 말한다. 그렇다면 이 단순화된 핵심만을 포함하는 언어로 함수형 언어의 핵심을 이해할 수 있지 않을까? 이게 바로 람다 대수(Lambda Calculus)의 역할이다.[2]
람다 대수는 딱 세 종류의 표현식만을 가지고 있다.
- 변수 (xx, yy, …\ldots)
- 매개변수 xx에 인자를 받아 한 표현식 MM(함수의 몸체)을 계산하는 함수 (λx→M\lambda x\to M)
- 어떤 표현식 LL의 결과 함수를 인자 NN으로 호출 (L NL\ N)
이후의 설명에서는 MM 과 NN, 그리고 LL이라는 이름을 임의의 표현식을 나타내기 위해 사용할 것이다. 람다 대수가 어떤 것들을 표현할 수 있는가? 앞에서 말했듯이 람다 대수는 함수의 인자와 함수 호출의 결과가 모두 함수인 표현식을 포함한다. 예를 들어 λx→(λy→y)\lambda x \to (\lambda y \to y) 는 매개변수 xx에 인자를 받아 함수 λy→y\lambda y \to y를 되돌려주는 함수이고, λx→(x (λy→y))\lambda x \to (x\ (\lambda y \to y))는 매개변수 xx에 함수인 인자를 받아 그 함수를 (λy→y\lambda y \to y를 인자로 사용하여) 호출하는 함수이다.
람다 대수(Lambda Calculus)의 평가(Evaluation)
이제 문제는
그래서 람다 대수의 표현식이 하는 일이 뭔데?
이다. 위의 표현식에 대한 소개는 산수로 말하자면 x+yx + y와 같이 연산자(++)와 연산항(xx와 yy)로부터 얻어지는 문법만을 설명하고 있고, 3+53 + 5와 같은 구체적인 표현식을 계산해서 88이라는 결과 값을 내놓는 방식을 설명하고 있지 않다. 이런 표현식으로부터 값을 얻어내는 것을 언어의 "평가 절차"("Evaluation Procedure")라고 한다. 람다 대수의 평가 절차를 설명하는 것은 어렵지 않다. 적어도 표면적으로는 말이다.
- 함수는 이미 값이다.
- 함수 λx→M\lambda x \to M을 NN으로 호출하면 MM에 등장하는 모든 xx을 NN으로 치환(Substitute)하고 결과 표현식의 평가를 계속한다.
이는 겉으로 보기에는 말이 되는 설명처럼 보인다. 하지만 이 설명을 실제로 해석기(Interpreter)로 구현하려고 시도한다면 이 설명이 사실 여러 세부사항을 무시하고 있다는 점을 깨닫게 될 것이다.
- 함수 호출 L NL\ N에서 LL이 (아직) λx→M\lambda x \to M 꼴이 아닐 때는 어떻게 해야하지?
- 함수 호출 (λx→M) N(\lambda x \to M)\ N에서 NN을 먼저 평가하는 게 낫지 않나? xx가 MM에 여러번 등장한다면 NN을 여러번 평가해야 할텐데?
첫번째 문제는 비교적 간단히 해결할 수 있다. LL을 먼저 평가해서 λx→M\lambda x \to M 꼴의 결과 값을 얻어낸 뒤에 호출을 실행하면 되기 때문이다. 반면에 두번째 질문은 좀 더 미묘한 문제를 가지고 있다. 함수 호출의 평가에서 발생하는 이 문제에 구체적인 답을 하기 위해서는 값에 의한 호출(Call-By-Value, CBV)와 이름에 의한 호출(Call-By-Name, CBN)이 무엇인지 이해해야 한다.
값에 의한 호출(Call-By-Value)? 이름에 의한 호출(Call-By-Name)?
앞에서 말한 함수 호출에서부터 발생하는 문제는 사실 함수형 언어에서만 발생하는 문제는 아니다. C와 같은 명령형 언어에서도 함수를 호출할 때 인자를 먼저 평가해야하는지를 결정해야하기 때문이다. 즉 이 문제는 함수를 가지고 있고 함수를 호출해야하는 모든 언어들이 가지고 있는 문제이다.
그렇다면 이 일반적인 문제를 어떻게 해결하는가? 대부분의 언어가 취하는 가장 대표적인 방식은 "값에 의한 호출"("Call-By-Value", "CBV")이라고 한다. 이 함수 호출 평가 절차에서는 함수의 몸체에 인자를 치환하기 전에[3] 인자를 먼저 평가한다. 이 방식을 사용하면 인자를 여러번 평가해야하는 상황을 피할 수 있다.
또 다른 방식은 "이름에 의한 호출"("Call-By-Name", "CBN")이라고 한다. 이 방식에서는 함수의 몸체에 인자를 우선 치환한 후 몸체를 평가한다. 몇몇 언어의 매크로(Macro)와 같은 기능이 이 방식을 사용한다. 얼핏 보기에는 CBN은 장점이 없어보인다. 그러나 함수가 인자를 사용하지 않을 경우는 CBN이 장점을 가진다는 것을 볼 수 있다. 극단적으로 평가가 종료되지 않는 표현식(Non-terminating expression)이 있다면[4] CBV는 종료하지 않고 CBN만이 종료하는 경우가 있음을 다음 예시를 통해 살펴보자. 표현식 (λx→(λy→y)) N(\lambda x \to (\lambda y \to y))\ N이 있다고 할 때, NN이 평가가 종료되지 않는 표현식이라고 하자. 이 경우 CBV를 따른다면 종료하지 않는 NN 평가를 먼저 수행하느라 이 표현식의 값을 얻어낼 수 없지만, CBN을 따른다면 λy→y\lambda y \to y라는 값을 손쉽게 얻어낼 수 있다. 바로 이런 상황 때문에
CBN은 CBV보다 일반적으로 더 많은 표현식들을 평가할 수 있다
고 말한다.
모호한 선택을 피하는 방법
두 방식의 장점을 모두 가질 수는 없을까? 다시 말해서, 어떤 상황에서는 이름에 의한 호출을 사용하고, 어떤 상황에서는 값에 의한 호출을 사용할 수 없을까? 이 질문에 답한 수많은 선구자들 가운데 폴 블레인 레비(Paul Blain Levy)가 내놓은 답인 "값 밀기에 의한 호출"("Call-By-Push-Value", "CBPV")은 함수형 언어의 평가를 기계 수준(Machine level)에서 이해하는데에 있어 강력한 도구를 제공한다. CBPV는 우선 "계산"("Computation")과 "값"("Value")을 구분한다.
- 계산 MM, NN, LL, …\ldots = 함수 λx→M\lambda x \to M 또는 함수 호출 L VL\ V
- 값 VV, UU, WW, …\ldots = 변수 xx
잠깐, 앞서서 함수형 언어에서 함수는 값이라고 하지 않았던가? 이는 값 밀기에 의한 호출에서 함수와 함수 호출을 종전과 전혀 다르게 이해하기 때문이다. 함수 λx→M\lambda x \to M는 스택(Stack)에서 값을 빼내어(Pop) xx라는 이름을 붙인 후 MM을 평가하는 것이고, 함수 호출 L VL\ V는 스택에 값 VV를 밀어넣고(Push)[5] LL을 평가하는 것이다. 따라서 함수 λx→M\lambda x \to M는 평가의 결과가 아닌 추가적인 평가가 가능한 표현식이 된다. 이 구분을 간결하게 설명하는 것이 다음의 CBPV 표어이다.
값은 "~인 것"이다. 계산은 "~하는 것"이다.
그렇지만 함수형 언어이기 위해서는 함수를 값으로 취급할 수 있어야 한다고 했지 않은가? 그렇다. 이를 위해 CBPV는
계산을 강제한다면(force\mathbf{force}) 계산 MM를 하는 지연된 계산인 값 thunk(M)\mathbf{thunk}(M)
을 추가로 제공한다. 이 둘 (force(V)\mathbf{force}(V)와 thunk(M)\mathbf{thunk}(M))을 다음과 같이 문법에 추가할 수 있다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V)
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
CBPV를 완성하기 위해 필요한 마지막 조각은 계산을 끝내는 법이다. 현재까지 설명한 λx→M\lambda x \to M와 L VL\ V 그리고 force(V)\mathbf{force}(V) 는 모두 다음 계산을 이어서 하는 표현식이고, 계산을 끝내는 방법을 제공하지는 않는다. 예를 들어 λx→M\lambda x \to M의 평가는 스택에서 값을 빼내고 계산 MM의 평가를 이어한다. 그렇다면 계산의 끝은 무엇인가? 결과 값을 제공하는 것이다. 이를 위해 return(V)\mathbf{return}(V)를 계산에 추가하고, 이 결과 값을 사용할 수 있도록 M to x→NM\ \mathbf{to}\ x \to N (계산 MM을 평가한 결과 값을 xx라고 할 때 계산 NN을 평가하는 계산) 또한 계산에 추가하면 다음의 완성된 CBPV를 얻는다.
- 계산 = λx→M\lambda x \to M 또는 L VL\ V 또는 force(V)\mathbf{force}(V) 또는 return(V)\mathbf{return}(V) 또는 M to x→NM\ \mathtt{\mathbf{to}}\ x \to N
- 값 = xx 또는 thunk(M)\mathbf{thunk}(M)
이제 CBPV를 얻었으니 원래의 목표로 돌아가보자. 어떻게 CBV 호출과 CBN 호출을 CBPV로 설명할 수 있을까?
- CBV 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 return(thunk(λx→M))\mathbf{return}{(\mathbf{thunk}(\lambda x \to M))}과 L to x→N to y→force(x) yL\ \mathbf{to}\ x \to N\ \mathbf{to}\ y \to \mathbf{force}(x)\ y로 표현할 수 있다. 즉, CBPV의 관점에서 CBV의 함수는 지연된 원래 계산 λx→M\lambda x \to M을 값으로 되돌려주는 계산으로 이해할 수 있고, 함수 호출 L NL\ N은 함수 부분 LL을 먼저 평가하고 NN을 평가한 뒤 NN의 계산 결과 yy를 스택에 밀어넣고 지연된 계산인 함수 부분 xx의 계산을 강제하는(force(x)\mathbf{force}(x)) 것으로 이해할 수 있다.
- CBN 함수 λx→M\lambda x \to M와 호출 L NL\ N이 있다면, 이를 λx→M\lambda x \to M(단, 변수 xx의 모든 사용을 force(x)\mathbf{force}(x)로 치환함)과 L thunk(N)L\ \mathbf{thunk}(N)로 표현할 수 있다. 즉, CBPV의 관점에서 함수 호출은 L NL\ N은 지연된 NN을 스택에 밀어넣은 뒤 LL의 계산을 이어가는 것으로 볼 수 있다. 이 지연된 NN은 이후에 스택에서 빼내어져 어떤 이름 xx가 붙은 뒤, 이 변수가 사용될 때에야 비로소 계산된다.
다소 설명이 복잡할 수 있으나, 단순하게 말해서 CBPV는 CBV에 따른 상세한 평가 순서와 CBN 따른 상세한 평가 순서를 세부적으로 설명할 수 있는 충분한 기능을 모두 갖추고 있으며, 이를 통해 CBV 함수 호출과 CBN 함수 호출을 모두 설명할 수 있다는 이야기이다.
기계 수준(Machine level)에서의 Call-By-Push-Value의 장점
앞에서는 CBPV가 CBV와 CBN를 모두 설명할 수 있음을 다뤘다. 그러나 CBPV는 프로그래머(Programmer)가 직접 사용하기에는 과도하게 자세한 세부사항들을 포함하고 있기에, 프로그래머가 직접 CBPV를 써서 CBV와 CBN의 구분을 조율하기에는 적합하지 않다. 그렇다면 어느 수준에서 CBV와 CBN을 혼합해 사용할 때 도움을 줄 수 있을까? 바로 람다 대수를 기계 수준으로 컴파일(Compile)할 때이다. 이때는 CBPV가 가진 자세한 세부사항의 표현력이 굉장히 유용해진다.
예를 들어 람다 대수를 기계 수준으로 변환할 때 흔히 필요한 것 중 하나인 항수 분석(Arity analysis)에 대해 이야기해보자. 항수 분석은 함수가 하나의 인자를 받은 뒤 실행되어야 하는지, 혹은 두 인자를 모두 받아 실행되어야 하는지 등을 확인하여 이후에 그에 걸맞는 최적화된 기계어(Machine language)를 생성할 수 있게 도와주는 분석 작업이다. 평범한 람다 대수에서는 항수 분석의 결과를 직접적으로 표현하기 어렵다. 예를 들어 람다 대수의 λx→(λy→y)\lambda x \to (\lambda y \to y)의 경우 이 함수가 xx와 yy를 모두 받아 yy를 되돌려주는 함수인지 (항수가 2인 함수인지), 혹은 xx를 받아 λy→y\lambda y \to y라는 함수를 되돌려주는 함수인지 (항수가 1인 함수인지) 구분할 수 없다. 그러나 이를 CBPV로 변환한 λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))나 λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 각각이 무엇을 뜻하는지 분명히 이해할 수 있다.
- λx→(λy→return(y))\lambda x \to (\lambda y \to \mathtt{return}(y))는 두 변수 xx와 yy를 스택에서 빼낸 뒤 yy의 값을 되돌려주는 함수(항수가 2인 함수)이다.
- λx→return(thunk(λy→return(y)))\lambda x \to \mathtt{return}(\mathtt{thunk}(\lambda y \to \mathtt{return}(y)))는 변수 xx를 스택에서 빼낸 뒤 지연된 계산 λy→return(y)\lambda y \to \mathtt{return}(y)를 돌려주는 함수(항수가 1인 함수)이다.
이런 장점을 바탕으로 CBPV를 더 발전시킨 "언박싱한 값에 의한 호출"("Call-By-Unboxed-Value")을 GHC 컴파일러의 중간 언어(Intermediate language)로 구현하는 것에 대한 논의가 현재 진행되고 있으며 앞으로 더 많은 함수형 컴파일러들이 관련된 중간 언어를 채용하기 시작할 것으로 보인다.
마치며
이 글에서는 함수형 언어의 핵인 람다 대수를 간단히 설명하고 람다 대수를 평가하는 방법에 대해서 다루어보았다. 특히 그 중 값 밀기에 의한 평가(Call-By-Push-Value, CBPV)가 무엇이며 CBPV가 다른 대표적인 두 방법(CBV, CBN)을 어떻게 표현할 수 있는지, 그리고 CBPV의 장점이 무엇인지에 대해서도 다루어 보았다. 이 글에서 미처 다루지 못한 중요한 주제는 CBPV를 기계에 가까운 언어로 번역해보는 것이다. 여기에서는 글이 너무 복잡해지는 것을 피하기 위해 제했으나, CBPV의 장점에서 살펴봤듯 이는 CBPV에 있어 핵심 주제 중 하나이기 때문에 이후에 다른 글을 통해서라도 이 주제를 소개할 기회를 가지고자 한다. 이 글이 CBPV에 대한 친절한 소개글이었기를 바라며 이만 줄이도록 하겠다.
결과 값(Value)을 가지는 언어 표현을 말한다. 예를 들어 1+11 + 1은 22라는 값을 가지는 표현식이지만 (JavaScript의)
let x = 3;나 (Python의)def f(): ...은 그 자체로는 값이 없기 때문에 표현식이 아니다. ↩︎다만 실제 역사에서는 람다 대수의 이해와 발견이 함수형 언어의 개발보다 먼저 이루어졌다. 이런 역사적 관점에서는 (이미 많은 수학자들이 이해하고 있던) 람다 대수에 여러 기능을 추가한 것이 바로 함수형 언어라고 볼 수 있다. ↩︎
프로그래밍 언어(Programming Language)는 실제로는 치환을 사용하지 않고 환경(Environment)을 사용하는 경우가 더 많지만 설명의 편의를 위해 다른 언어들 또한 환경 대신 치환에 기반해 평가한다고 가정하겠다. ↩︎
앞서 설명한 람다 대수에서는 이를 쉽게 얻을 수 있다. 오메가(Ω\Omega)라고 부르는 표현식인 (λx→x x) (λx→x x)(\lambda x \to x\ x)\ (\lambda x \to x\ x)의 평가는 값에 의한 호출을 따르든 이름에 의한 호출을 따르든 종료되지 않는다. ↩︎
바로 이 함수 호출을 값 밀기에 기반해 해석하는 데에서 CBPV의 이름이 유래했다. ↩︎
![]() @lionhairdino
@lionhairdino @xtjuxtapose 마침 방금 공개한 글이 이런 이해와 관련이 있어보이네요.
오, 선 하트 박고, 읽으러 갑니다. ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4) @xtjuxtapose
저도 두 가지 쟁점 모두 동의하는 편입니다. 그리고, 별개의 이야기입니다만, $ 를 가르칠 때에는 그냥 문법이라고 가르치는 게 학습자의 이해와 응용이 압도적으로 빠르고 좋았습니다.
"이건 여기서부터 뒤로는 다 괄호로 감싸겠다는 뜻이라고 생각하세요."
이러면 한 방에 설명이 끝나고, 필요성이나 편리성에 대해서도 알아서들 납득하는 것이죠. 연산자 우선순위나 좌결합 우결합 등은 그게 되고 나서 얘기하고요. 그러면 "아, 이게 그래서 이렇게 되는 거였군요?" 하면서, 훨씬 쉽게 이해합니다. 이걸 거꾸로 좌결합 우결합 어쩌고부터 가르치려고 하면 다들 꾸벅꾸벅 졸아요... ㅋㅋ ㅠㅠ
(결국 "모나드란 무엇인가"부터 배우면/가르치면 안 된다는 주장과 같은 맥락입니다.)
RE: https://hackers.pub/@bgl/01963c3b-98fa-7432-a62f-0d2dfc0691bf
함수형을 공부하기 전, 함수 작업?의 대상을 {함수, 인자}로만 인식했었는데, {함수, 인자, 적용}으로 인식하기 시작하면서 편해지는 게 많아졌습니다. 그런데 이게 편한 이유가 다른 배경 지식이 생겨서 그런 건지, 이 길로 가는게 쉬운 길이어서 그런 건지는 잘 모르겠습니다. 여기서 시작하면 $와 <$>가 자연스러워 보였습니다. 혼자 결론에 도달하고는, 누군가가 처음 공부할 때 알려줬으면 좋았겠는데 싶었습니다. 그냥 혼자 생각입니다.
꾸벅 꾸벅 조는 건 완전 동의입니다. 제가 혼자 그 공부하면서 졸았습니다. @xtjuxtapose
![]() @lionhairdino 조만간 구현해 보도록 하겠습니다.
@lionhairdino 조만간 구현해 보도록 하겠습니다.
"기능을 빨리 내놓으세요"는 절대 아니고, 필요한 기능, 아이디어들 리스트업하는 의미입니다. 깃헙 리포가서 이슈 남겨야 하는데, 영어로 남기려니, 사소한 거는 멈칫합니다. 다음 번엔 꼭 이슈로 가겠습니다. ![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)
파폭에서 탭 고정pinning을 해서 SNS들을 쓰고 있는데요. 알림 박스의 빨간점이, 다른 서비스들 처럼 파비콘에도 찍히면 좋겠는데요.(그림에서 링크드인은 새 글도 있고, DM도 있고) 아직 기능이 없으면 조용히 기다리려 했는데, 알림 박스 기능이 이미 있으니, 뭔가 어렵지 않은 작업으로 되지 않을까 싶어 글 남깁니다.
수건 도착
하스켈 코드 포매터 stylish-haskell을 잘 쓰고 있습니다. Vim에서 :%!stylish-haskell이라고 입력하는 방식으로 사용하는데요, 코드에 문제가 있을 경우 코드 전체가 지워지고 다음과 같은 문자열로 대체됩니다.
<string>:1:18: error: [GHC-58481] parse error on input `!'Vim에서 작업 중이므로 단순히 u를 눌러서 취소하면 되긴 합니다만 혹시 다른 방법이 있을까요?
![]() @curry박준규 보통 HLS에 붙어 있는 것 쓰는데, 그리 단독으로도 쓰는 군요. 근데, 코드를 지운다니 살짝 무서운데요.
@curry박준규 보통 HLS에 붙어 있는 것 쓰는데, 그리 단독으로도 쓰는 군요. 근데, 코드를 지운다니 살짝 무서운데요.
![]() @lionhairdino 이게 이제서야… 허허허.
@lionhairdino 이게 이제서야… 허허허.
HLS 관리자분이 해펍에 계시니, 원하시는 게 있으면 적극적으로 소통해 보세요. ![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)
![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee) ![]() @lionhairdino 파이어폭스에서도 타 플랫폼에선 Windows Hello나 iCloud 패스키 등을 정상적으로 지원하는데, 아마 NixOS를 사용 중이셔서 불러올 플랫폼 API가 없는 것 아닐까 싶습니다 😅
@lionhairdino 파이어폭스에서도 타 플랫폼에선 Windows Hello나 iCloud 패스키 등을 정상적으로 지원하는데, 아마 NixOS를 사용 중이셔서 불러올 플랫폼 API가 없는 것 아닐까 싶습니다 😅
잘 모르는데요. 아마도 usb 하드웨어 키 같은 것만 지원하고, 아직 블루투스로 스마트 폰의 패스키와 연동은 안된다는 것 같습니다. 말씀하신 플래폼 API라는 게 NixOS용이 있는지 찾아 보겠습니다. 답 주셔서 감사합니다~ @xiniha
![]() @hongminhee洪 民憙 (Hong Minhee)
@hongminhee洪 民憙 (Hong Minhee)
하스켈 언어 서버HLS 2.10.0.0에 go to implementation 기능이 생겼네요. .cabal 파일 지원도 많이 들어갔다 합니다.
글을 한 방에 써야되는데, 빠진 말이 생각나 댓을 달면, 타임라인에 중복이 너무 많이 나와 진상 유저가 된 느낌이 드네요 ^^;; 댓의 원 글이 안나와야 되는 것 아닐까 싶어요. 클릭해서 들어가면 타래를 보고... 개인 의견입니다.
![]() @hongminhee洪 民憙 (Hong Minhee) 아이폰은 문제 없이 잘 됩니다. 파이어폭스에서는 yubikey(USB지문?)같은 게 있어야 되는 건지, 아래 키등록 화면에서 넘어가길 않습니다. 아마도 해커스펍 구현 문제는 아닌 걸로 보입니다만, 지식이 없어 아직 리포트를 쓸만하게 못하겠습니다.
@hongminhee洪 民憙 (Hong Minhee) 아이폰은 문제 없이 잘 됩니다. 파이어폭스에서는 yubikey(USB지문?)같은 게 있어야 되는 건지, 아래 키등록 화면에서 넘어가길 않습니다. 아마도 해커스펍 구현 문제는 아닌 걸로 보입니다만, 지식이 없어 아직 리포트를 쓸만하게 못하겠습니다.
![]() @hongminhee洪 民憙 (Hong Minhee) 대부분 USB 장비는 없을테고, 스마트폰을 위한 QR화면이 떠야 될 것 같은데, 그 건 해펍에서 지원해줘야 되는 거지요?
@hongminhee洪 民憙 (Hong Minhee) 대부분 USB 장비는 없을테고, 스마트폰을 위한 QR화면이 떠야 될 것 같은데, 그 건 해펍에서 지원해줘야 되는 거지요?
![]() @lionhairdino 혹시 어떤 식으로 안 되는지 알 수 있을까요? 오류 메시지라든가… Hackers' Pub 구현의 문제일 수 있어서요.
@lionhairdino 혹시 어떤 식으로 안 되는지 알 수 있을까요? 오류 메시지라든가… Hackers' Pub 구현의 문제일 수 있어서요.
![]() @hongminhee洪 民憙 (Hong Minhee) 아이폰은 문제 없이 잘 됩니다. 파이어폭스에서는 yubikey(USB지문?)같은 게 있어야 되는 건지, 아래 키등록 화면에서 넘어가길 않습니다. 아마도 해커스펍 구현 문제는 아닌 걸로 보입니다만, 지식이 없어 아직 리포트를 쓸만하게 못하겠습니다.
@hongminhee洪 民憙 (Hong Minhee) 아이폰은 문제 없이 잘 됩니다. 파이어폭스에서는 yubikey(USB지문?)같은 게 있어야 되는 건지, 아래 키등록 화면에서 넘어가길 않습니다. 아마도 해커스펍 구현 문제는 아닌 걸로 보입니다만, 지식이 없어 아직 리포트를 쓸만하게 못하겠습니다.
패스키 개념이 없어, 검색에 의존해서 NixOS, 파이어폭스, 인증 장비는 스마트폰으로 어찌 해보려 했더니, 안되는 건가 봅니다. PC에서 기존 메일 방식으로 로그인 하고, 아이폰에서는 패스키로 로그인 해야겠습니다.
아주 오래 전, 스콧마이어스 책을 곽용재님 번역으로 봤었는데, (아는 분은 아니고, 이 분 C++ 번역 책을, 번역책으론 드물게 좋아합니다.) 오, 스콧의 정리가 여러 사람의 시간을 살리겠구나.. 했었습니다. 근데, 지금 보면, Effective C ++ 책에 있는 내용들은, 왜 프로그래머가 조심하고, 조심하게 만들었을까 싶은 것들이 수두룩 합니다. 이런 것들은 기계가(혹은 언어 스펙이) 알아서 해야 할 일들 아닌가 싶습니다.
예전엔 스콧의 테크닉쯤은 미리 알고 있는 게 숙련자였는데, 모던? 언어들을 만지는 지금은 그 테크닉들이 다 원시적으로 보입니다. 한 때는 밥벌이에 필수 지식이었을텐데요.
오, 아직 판매되고 있네요. C++은 아직 팔팔한 현역인데, 오래된 책을 보다 헛소리 했습니다.
아주 오래 전, 스콧마이어스 책을 곽용재님 번역으로 봤었는데, (아는 분은 아니고, 이 분 C++ 번역 책을, 번역책으론 드물게 좋아합니다.) 오, 스콧의 정리가 여러 사람의 시간을 살리겠구나.. 했었습니다. 근데, 지금 보면, Effective C ++ 책에 있는 내용들은, 왜 프로그래머가 조심하고, 조심하게 만들었을까 싶은 것들이 수두룩 합니다. 이런 것들은 기계가(혹은 언어 스펙이) 알아서 해야 할 일들 아닌가 싶습니다.
예전엔 스콧의 테크닉쯤은 미리 알고 있는 게 숙련자였는데, 모던? 언어들을 만지는 지금은 그 테크닉들이 다 원시적으로 보입니다. 한 때는 밥벌이에 필수 지식이었을텐데요.
비디오 테스트인데, 성급히 하트를 날렸습니다. 근데, 홈서버인데, 영상도 버틸까요... 제가 걱정할 일은 아닌데, 걱정이 되네요? ㅎㅎ
![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4) ![]() @kodingwarriorJaeyeol Lee
@kodingwarriorJaeyeol Lee ![]() @lionhairdino 아아 어떤 느낌인지 상상이 갑니다. 저는@parksb
님이 하신것처럼 맥주가 차있으면 좋겠다싶어 H 중간 막대를 위로 올렸습니다.
@lionhairdino 아아 어떤 느낌인지 상상이 갑니다. 저는@parksb
님이 하신것처럼 맥주가 차있으면 좋겠다싶어 H 중간 막대를 위로 올렸습니다.
H가 컵이고, P가 손잡이어야 하는데, H가 컵 모양이 잘 안나와서, 포기하고 그냥 맥주에 담가 버렸습니다. (근데 호스트분 아주 근거리에 디자이너분 계신 거 아닌가 모르겠습니다.) ![]() @ailrunAilrun (UTC-5/-4)
@ailrunAilrun (UTC-5/-4)
가로 스크롤 원인 2 - 긴 URL
슬슬 해커스펍 svg 로고를 찾을 때가 오고 있습니다.
"게시글만"에 이틀만 새 글이 없어도 고파합니다. 누가 읽을거리 안 던져 주시나...
호스트분 얼굴이 대문짝만하게 나와, 아 깜짝이야 했습니다.
아이폰 사파리 가로 스크롤 원인
@fwangdo 퐝도님, 반갑습니다. 어서오세요~~
여기에서는 트위터보다 조금 더 편하게 글을 써보려고 합니다. 해커스펍 가입해놓고 글 하나 안 올렸었네요.
![]() @d01c2Hyunjoon Kim 오랜만입니다~ 커피 안머는 사람은 돌케라고 읽지 않을까요? 계속 연을 이어갔으면 했던 분들 하나 둘 보이니 좋네요.
@d01c2Hyunjoon Kim 오랜만입니다~ 커피 안머는 사람은 돌케라고 읽지 않을까요? 계속 연을 이어갔으면 했던 분들 하나 둘 보이니 좋네요.
![]() @lionhairdino 명사형 종결 어미는 옛날에도 글에서는 종종 쓰지 않았나요? 주로 통지서 같은 데서… 물론 입말로도 그러는 건 요즘의 현상 같습니다.
@lionhairdino 명사형 종결 어미는 옛날에도 글에서는 종종 쓰지 않았나요? 주로 통지서 같은 데서… 물론 입말로도 그러는 건 요즘의 현상 같습니다.
![]() @hongminhee洪 民憙 (Hong Minhee) 관공서는 아직 많이 쓸 겁니다. 국가 운영 재단, 기금 같은데 서류 (사업자 기획 같은 것들) 낼 때도, 그렇게 쓰라고 가이드하기도 합니다. 채팅할 때 존댓말과 반말 사이가 애매해 쓴다고 느낄 정도로, 요즘 세상의 저는 선호하지 않고 있습니다. ㅎ
@hongminhee洪 民憙 (Hong Minhee) 관공서는 아직 많이 쓸 겁니다. 국가 운영 재단, 기금 같은데 서류 (사업자 기획 같은 것들) 낼 때도, 그렇게 쓰라고 가이드하기도 합니다. 채팅할 때 존댓말과 반말 사이가 애매해 쓴다고 느낄 정도로, 요즘 세상의 저는 선호하지 않고 있습니다. ㅎ